Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 7.Problemas - Ex. 6
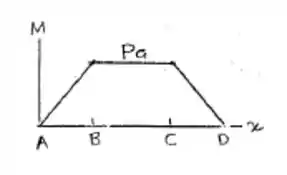
Desenhar os diagramas de força cortante e de momento fletor para a viga com o carregamento mostrado.
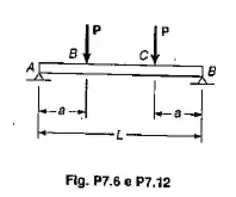
Passo 1
Para iniciarmos a questão, vamos calcular as reações no ponto A e D analisando os momentos. OBS: vamos adotar o sentido anti-horario como positivo.
Fazemos o mesmo analisando o momento em relação ao outro lado:
Passo 2
Fazendo a anaise do cortante e do momento fletor entre A e B
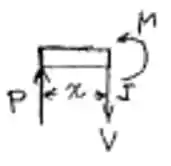
Vamos então fazer a análise das forças para montarmos o diagrama de forças cortantes. Vou adotar as forças pra cima como positivas.
Fazemos agora a mesma análise para o momente. Adotaremos o sentido anti-horário como o positivo.
Passo 3
Fazendo a anaise do cortante e do momento fletor entre B e C
Vamos então fazer a análise das forças para montarmos o diagrama de forças cortantes. Vou adotar as forças pra cima como positivas.
Fazemos agora a mesma análise para o momente. Adotaremos o sentido anti-horário como o positivo.
Passo 4
Fazendo a anaise do cortante e do momento fletor entre C e D
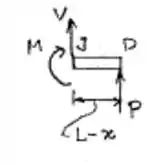
Vamos então fazer a análise das forças para montarmos o diagrama de forças cortantes. Vou adotar as forças pra cima como positivas.
Fazemos agora a mesma análise para o momente. Adotaremos o sentido anti-horário como o positivo.
Passo 5
Podemos agora montar nossos diagramas. Do cortante
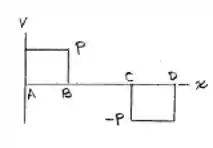
Os momentos máximos que temos são nos pontos B e C
