Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 5.Problemas - Ex. 20

Para uma viga de madeira com a seção transversal mostrada, determinar a maior força cortante vertical admissível, se a tensão de cisalhamento não deve exceder a 1035   k P a .

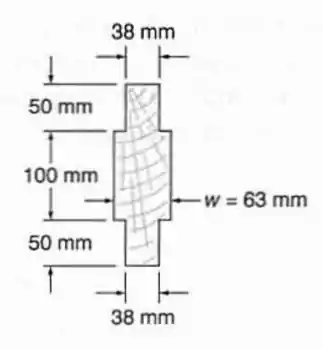
Passo 1

Se o problema pede a maior força cortante admissível nós temos que lembrar que a força cortante está ligado à tensão de cisalhamento!! É o famoso “tau vê qit”

τ m = V Q I t

Desta forma nós queremos o V que é a força cortante enquanto o problema deu a tensão de cisalhamento máxima τ m , além da geometria da figura, que por meio da geometria vamos achar o momento de inércia I , o momento estático Q e a espessura t .

Passo 2

Vamos utilizar a geometria da figura para achar o momento de inércia.

I = 2 ⋅ I 1 + I 2

I 1 = 1 12 b h 3 + A d ²

I 1 = 1 12 ⋅ 0,038 ⋅ 0,050 3 + 0,038 ⋅ 0,050 ⋅ 0,075

I 1 = 1,43 × 10 - 4   m 4

I 2 = 1 12 b h 3

I 2 = 1 12 ⋅ 0,063 ⋅ 0,100 3

I 2 = 5,26 × 10 - 6   m 4

I = 2 ⋅ 1,43 × 10 - 4 + 5,26 × 10 - 6

I = 2,91 × 10 - 4   m 4

Passo 3

Agora só precisamos do momento estático Q , que será calculado de maneira semelhante ao momento de inércia. Adotando qualquer uma das metades (superior ou inferior):

Q = ∑ A ⋅ Y -

Vamos dividir a peça em 3 pedaços e teremos:

Q = 2 ⋅ Q 1 + Q 2

Q 1 = 0,038 ⋅ 0,050 ⋅ 0,075

Q 1 = 1,43 × 10 - 4   m 3

Q 2 = 0,063 ⋅ 0,050 ⋅ 0,025

Q 2 = 7,88 × 10 - 5   m 3

Substituindo:

Q = Q 1 + Q 2

Q = 2 ⋅ 1,43 × 10 - 4 + 7,88 × 10 - 5  

Q = 3,65 × 10 - 4   m 3

Passo 4

Agora é só substituir na nossa formulinha como falado no primeiro passo!

τ m = V Q I t

Onde t é a espessura t = 63   m m .

1,035 × 10 6 = V ⋅ 3,65 × 10 - 4 2,91 × 10 - 4 ⋅ 0,063

V = 52   k N

Resposta

V = 52   k N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A viga mostrada foi feita colando-se várias tábuas. Sabendo que a viga está sujeita a uma força cortante de 5 kN, determine a tensão de cisalhamento média nas juntas coladas (a) em A (b) em B.
A viga mostrada na figura foi feita pregando-se várias tábuas e está sujeita a uma força cortante de 8 kN. Sabendo que os pregos estão espaçados longitudinalmente a cada 60 mm em A e a cada 25 mm em B
Uma viga de alumínio extrudada tem a seção transversal mostrada na figura. Sabendo que a força cortante vertical na viga é 150 kN, determine a tensão de cisalhamento no (a) ponto a e (b) ponto b.
Para a viga construída no Prob. 6.1, determine a tensão de cisalhamento admissível se o espaçamento entre cada par de pregos é s = 45 mm
Três pranchas de 50 x 100 mm são pregadas juntas para formar um viga que é submetida a uma força cortante de 1500 N. Sabendo que a tensão de cisalhamento admissível em cada prego é de 400 N, determine