Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 4.Problemas - Ex. 114

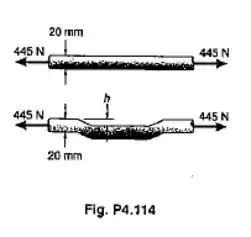
Um desvio h deve ser executado em uma barra circular maciça. Sabendo-se que a máxima tensão, depois desse desvio ser executado, não deve exceder três vezes a tensão na barra quando era reta, determinar: (a) o maior desvio que pode ser usado; (b) a corrensdente tenssão máxima na barra.

Passo 1

Bom, para a σ teremos

σ 0 = P A = 445 π × 0,01 2 = 1,416   M P a

O enunciado nos diz que a tensão máxima não deve passar de 3 vezes a tensão da barra, logo (respondendo já a letra b, haha)

σ m a x = 3 × σ 0 = 4,248   M P a

Para o somatório do momento teremos

M = 445 × h

E por último a inércia da circunferência

I = π × r 4 4 = π × 0,01 4 4 = 7,85 × 10 - 9 m 4

Passo 2

A letra a nos pergunta quanto vale h, para isso faremos

σ m a x = σ 0 + M c I → 1,416 × 10 6 + 445 × h × 0,01 7,85 × 10 - 9 = 4,248 × 10 6

Isolando o h encontramos

h = 4,998 × 10 3   m

Resposta

  a )   h = 4,998     m m

b )   σ m a x = 4,248   M P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A barra curva mostrada tem a seção transversal de 30 x 30 mm. Sabendo que a tensão admissível na compressão é 175 MPa, determine a maior distância a admissível.
Para o anel aberto mostrado na figura, determine a tensão no (a) ponto A e (b) ponto B.
Sabendo que a máxima tensão admissível é 45 MPa, determine a intensidade do maior momento M que pode ser aplicado aos componentes mostrados.
Três chapas são soldadas umas às outras para formar a barra curva mostrada na figura. Para o carregamento dado, determine a distância e entre a linha neutra e o centroide da seção transversal.
Três chapas são soldadas umas às outras para formar a barra curva mostrada na figura. Para o carregamento dado, determine a distância e entre a linha neutra e o centroide da seção transversal.(Obs: pe