Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 4.Problemas - Ex. 113

Resolva o problema 4.112, assumindo que a carga de 20 kN é removida.

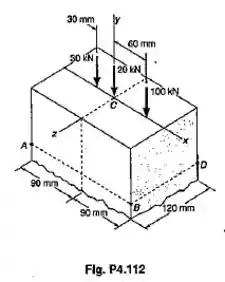
Passo 1

Teremos para área superior a mesma coisa da questão anterior

A = 0,12 × 0,18 = 0,216   m 2

Somatório de momentos (anti horário positivo) ainda igual a questçao anterior:

M c = - 30 × 30 + 60 × 100 = 5,1   k N . m

Para o momento de inércia exatamente igual a questão anterior também haha

I = b × h 3 12 = 0,12 × 0,18 3 12 = 5,832 × 10 - 5   m 4

Por último mas certamente não menos importante temos o σ 1 , onde finalmente teremos uma diferenã quando comparada a questão anterior, vamos remover a força de 20 kN.

σ 1 = - 30 × 10 3 + 100 × 10 3 0,0216 = - 130 × 10 3 0,0216 = - 6,019   M P a

Passo 2

Com isso já podemos comçar a calcular o que cada letra pede! Para a letra a o σ A T O T A L será dao por

σ A T O T A L = M c I = 5,1 × 10 3 × 0,09 5,832 × 10 - 5 - 6 , 019 × 10 6 = 1,815   M P a

Passo 3

Por último, para a letra (b) vamos ter simplesmente um sinal invertindo já que estamos agora trabalhando na outra ponta.

σ B T O T A L = - 5,1 × 10 3 × 0,09 5,832 × 10 - 5 - 6 , 019 × 10 6 = - 1 3,889   M P a

Resposta

a ) σ A t o t a l = 1,815   M P a

b )   σ B t o t a l = - 13,889   M P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O anel mostrado na figura tem um raio interno r 1 = 20,3m m e uma seção transversal circular de diâmetro d = 15,24m m . Sabendo que cada uma das forças de 534 N é aplicada ao centroide da seção transv
A barra mostrada tem seção transversal circular de 14 mm de diâmetro. Sabendo que a = 32m m , determine a tensão (a) no ponto A, (b) no ponto B.(Obs: o enunciado diz que o tubo tem 14 mm de diâmetro,
Resolva o problema 4.175 considerando que o anel tem um raio interno r 1 = 15,24m m e uma seção transversal circular de diâmetro d = 20,3m m .
Sabendo que a máxima tensão admissível é 45 MPa, determine a intensidade do maior momento M que pode ser aplicado aos componentes mostrados.
A barra mostrada tem seção transversal circular de 14 mm de diâmetro. Sabendo que a tensão admissível é de 38 MPa, determine a maior distância a permitida entre a linha de ação da força de 220 N e o p