Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 4.Problemas - Ex. 170
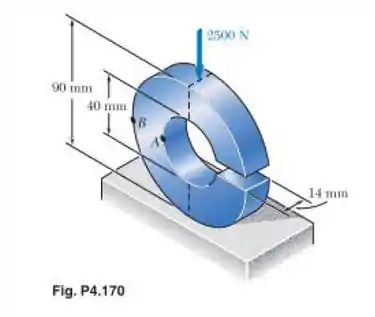
Para o anel aberto mostrado na figura, determine a tensão no (a) ponto A e (b) ponto B.
Passo 1
Tá legal! A primeira que devemos fazer é notar quais são o raio interno e externo do anel da figura, de modo que teremos:
Com isso, a espessura do anel será:
Agora vamos calcular o valor da área da seção transversal dessa seção, então teremos:
Agora, conforme vimos da Fig. 4.61 dessa seção, para a seção retangular de uma barra curvada, podemos encontrar o raio de superfície neutra através de:
Onde é o raio externo e é o raio interno. Dessa forma, substituindo os valores conhecidos para essa equação, chegamos em:
Passo 2
Agora vamos calcular a excentricidade, que é a distância entre o centroide e o eixo neutro da seção transversal, dessa forma, teremos:
Substituindo os valores conhecidos, teremos:
Agora podemos encontrar a tensão no ponto A pedida na letra (a) através da equação 4.71, somado a parcela da força exercida por P (que nesse caso é de compressão), então teremos:
Sabendo que podemos escrever o momento em função da carga aplicada e da distância até o centroide da seção dada, que nada mais é do que o raio médio que utilizamos no cálculo da excentricidade. Dessa forma, teremos:
Substituindo os valores conhecidos, teremos:
Então agora podemos substituir os valores conhecidos na equação de tensão e encontrar a tensão no ponto A:
Passo 3
Agora para a letra (b) vamos repetir os cálculos do passo 2, só que para o ponto B, onde teremos:
Então, utilizando novamente a equação 4.171, teremos:
E, substituindo os valores conhecidos, chegaremos em: