Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 4.Problemas - Ex. 171
Três chapas são soldadas umas às outras para formar a barra curva mostrada na figura. Para o carregamento dado, determine a distância e entre a linha neutra e o centroide da seção transversal.
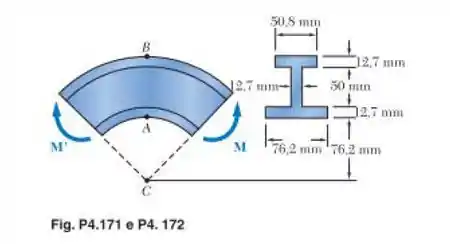
(Obs: perceba que esse enunciado está igual ao enunciado da questão 172, isso se deve a um erro de impressão na versão traduzida do livro, na verdade, a questão 171 pede para encontrarmos a tensão nos pontos A, B e no centroide da seção transversal. Para isso, precisamos de um valor de momento, que também não foi dado, então vamos assumir M = 1000 N.m)
Passo 1
Tá legal! Com as considerações a respeito do enunciado feitas, vamos dividir a seção transversal da viga em 3 partes, onde teremos:
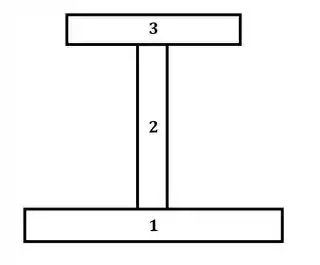
Agora nós vamos escrever a expressão que vamos utilizar para encontrar a distância do centro de curvatura C até a superfície neutra. Conforme vimos nessa seção, a equação para essa distância foi apresentada na equação 4.66
No entanto, nós dividimos nossa seção transversal em 3, então, nossa fórmula deverá levar em conta essas 3 seções separadas, para isso, faremos o somatório dos termos, chegando em:
Reescrevendo a expressão abrindo o termo dA e resolvendo, teremos:
Em que é a área da seção em análise, a sua espessura e o raio interno e o raio externo da seção transversal. Sendo assim, precisamos encontrar esses termos para todas as seções. Vamos precisar também da distância média do centroide da seção em estudo, dada por . Como temos uma seção composta, a equação 4.67, em somatório, se torna:
Passo 2
Vamos começar os cálculos pela primeira seção da figura do passo 1. Vamos calcular primeiro a sua área, que será dada por:
Agora vamos definir os raios interno e externo. Pela figura, o raio interno será:
E o raio externo, por sua vez, será:
Sendo assim, o raio médio da seção será:
Agora vamos encontrar os valores para a área 2. Sua área será:
Agora vamos definir os raios interno e externo. Pela figura, o raio interno será:
E o raio externo, por sua vez, será:
Sendo assim, o raio médio da seção será:
Agora vamos encontrar os valores para a área 3. Sua área será:
Agora vamos definir os raios interno e externo. Pela figura, o raio interno será:
E o raio externo, por sua vez, será:
Sendo assim, o raio médio da seção será:
Passo 3
Agora podemos calcular o R e lá do passo 1. Começando por R teremos:
Agora, para teremos:
Com esses dois valores, podemos encontrar a excentricidade da seção, que é a distância entre a linha neutra e o centroide da seção, através de:
Substituindo os valores conhecidos, chegamos em:
Passo 4
Com essas informações conseguimos encontrar a tensão no ponto A, através da equação 4.71, onde temos:
Substituindo os valores conhecidos, chegamos em:
Agora, repetindo os cálculos, só que para o ponto B, com , teremos:
E, por fim, calculando a tensão no centroide da seção, em , teremos: