Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 9.Problemas - Ex. 114
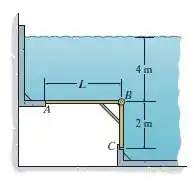
Se , detemrine a força que a comporta exerce sobre a tampa lisa em . A comporta é articulada em , livre em e tem de largura. A densidade da água é .
Passo 1
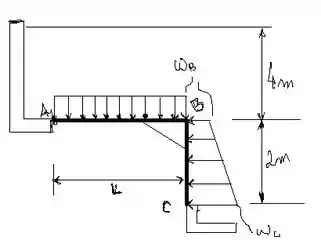
Vamos desenhar essa situação para entender melhor a questão. Como a tampa tem largura constante, a carga hidrostática na tampa pode ser representada por uma carga bidimensional.
Um cara chamado Pascal enunciou uma vez que, um fluido em repouso cria uma pressão em um ponto que é a mesma em todas as direções. A intensidade de , medida como uma força por área unitária, depende do peso específico ou densidade de massa do fluido e da profundidade do ponto a partir da superfície do fluido. Podemos escrever a expressão da pressão como:
Substituindo os valores dados no enunciado, temos a pressão igual a:
A intensidade de carga que a água causa na parede é dada por:
Passo 2
Vamos olhar o diagrama de corpo livre da comporta agora
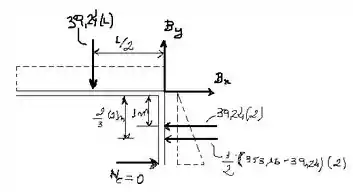
Para um corpo em equilíbrio, o somatório dos momentos em relação a um ponto deve ser igual a zero. Assim, assumindo como sentido positivo anti-horário, temos:
Resposta
A força resultante em é igual a: