Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 7.Problemas - Ex. 31
Determinar: a) Intensidade P de duas forças, dirigidas de baixo para cima, para que o máximo valor absoluto do momento fletor na viga seja tão pequeno quanto possível; b) a correspondente tensão normal máxima devido à flexão.
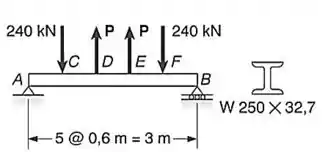
Passo 1
E ai gurizada tudo beleza? Espero que sim!!
O exercício pede para que possamos achar P, para isso vamos fazer o somatório de boinhas levando o P junto vem comigo que no caminho vou te explicando..
Partiu encontrar as reações :D ;)
Vamos considerar que VA=VB
Passo 2
- Agora vamos determinar a força cortante? Vem comigo!!!
Para realizarmos esse diagrama pensem comigo, eu falei para vocês antes que a seta para baixo é negativo certo? Lembrando da esquerda para a direita e detalhe IMPORTANTE, o exercício considerou que o centro é em “D”.
(Equação 1)
Agora temos que calcular o máximo em “B”:
(Equação 2)
Agora galera vamos igualar 2 com 1 para encontrarmos “P” ;)
Agora sim temos todas as cargas para podermos achar tensão normal máxima...
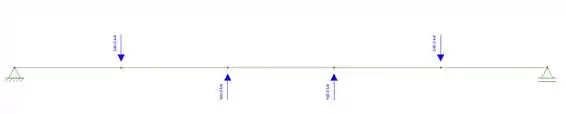
Passo 3
Vamos encontrar o esforço cortante, vem comigo :D
1° quadrante: VA= 80 KN
2° quadrante: 80-240= -160 KN
3° quadrante: -160+160= 0 KN
4° quadrante: 0+160= 160 KN
5° quadrante: 160-240= -80 KN
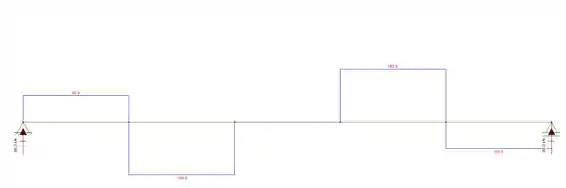
Agora vamos encontrar os momentos, vem comigo :p
MA=0
Gurizada notem que os demais valores dos cortantes se repetem, consequentemente ocorre com o momento, então fica a dica, calcula só para a metade e depois espelha ;)
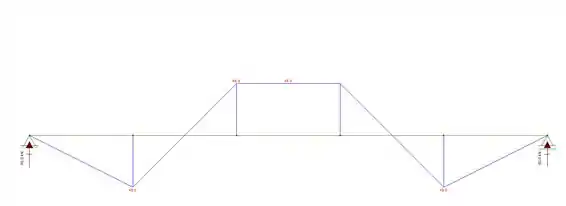
Ufaaaa agora podemos encontrar a tensão normal, mas antes precisamos verificar a inerciada viga (Iz) no livro, te dou 2 min .. obaa!! Agora vamos continuar :D