Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 5.Problemas - Ex. 138
Determine o centroide da área plana das figuras mostradas a seguir.
Passo 1
Nesse tipo de exercício, precisamos dividir a figura em algumas áreas que podemos calcular e encontrar os centros de gravidade, nesse caso, vamos subtrair a área embaixo da curva da área total conforme a figura a seguir:
Passo 2
Então, temos duas regiões, agora precisamos encontrar os valores das áreas e dos seus centros de massa, bem como o produto entre esses dois termos, então, agrupando todas essas informações na tabela a seguir, temos:
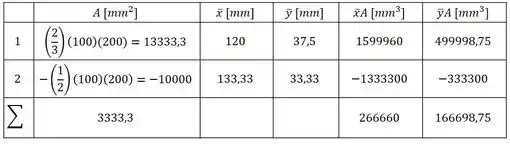
Passo 3
Agora ficou fácil, precisamos só usar as formulas mostradas nessa seção do livro, para temos:
Então, substituindo os valores da tabela do passo 2, temos:
Repetindo o processo para :
Substituindo os valores da tabela do passo 2:
Resposta
Exercícios de Livros Relacionados
Como são definidos o ângulo plano e o ângulo sólido? Quais são as respectivas unidades e símbolos no SI?
O que é um referencial inercial? Por que um referencial fixado à Terra não é inercial? E por que se adota esse referencial nos usuais problemas de engenharia
Quais são as dimensões (de base) das grandezas físicas momento de uma força, velocidade, aceleração e frequência
O que é Estática das Estruturas? Qual a importância dessa Estática
Qual é a diferença entre partícula e corpo? Como ambos têm massa finita e na realidade todos os corpos são deformáveis, por que adotar, por vezes, a hipótese de corpo rígido