Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 5.Problemas - Ex. 139
A moldura de um letreiro é fabricada com uma barra chata de aço fina cuja massa por unidade de comprimento é 4,73 kg/m. A moldura é sustentada por um pino em C e pelo cabo AB. Determine a tensão no cabo, a reação em C.
Passo 1
Beleza! Nesse exercício, precisamos primeiro encontrar o centro de gravidade da figura, para isso, separando a moldura em segmentos de linha, temos:
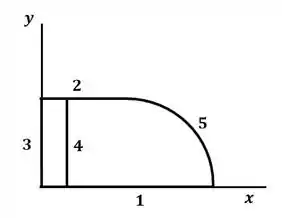
Passo 2
Então, temos cinco segmentos, agora precisamos encontrar os valores dos comprimentos e dos seus centros de massa, bem como o produto entre esses dois termos, então, agrupando todas essas informações na tabela a seguir, temos:
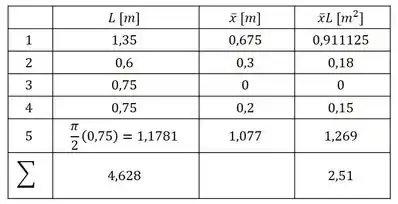
Agora ficou fácil, precisamos só usar as formulas mostradas nessa seção do livro, para temos:
Então, substituindo os valores da tabela do passo 2, temos:
Passo 3
Antes de usar as equações de equilíbrio, precisamos calcular o peso da moldura, que é dado por:
Substituindo os valores dados no enunciado e encontrados no passo 2:
Agora, o diagrama de corpo livre para o problema será:
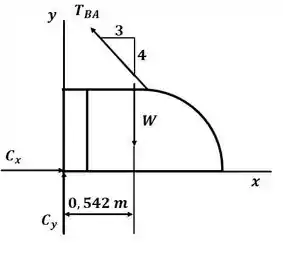
Aplicando o somatório de momento em relação ao ponto , temos:
Isolando e resolvendo, temos:
Agora, aplicando o somatório de forças na direção :
Isolando e substituindo o valor de encontrado:
E, finalmente, aplicando o equilíbrio na direção :
Isolando e substituindo o valor de e encontrados: