Enunciado
Mecânica e Resistência dos Materiais - Estatica das Estruturas por Humberto Lima Soriano- Ed: 3º - Capítulo 1.10 - Ex. 11
Como são definidos o ângulo plano e o ângulo sólido? Quais são as respectivas unidades e
símbolos no SI?
Passo 1
Primeiro vamos definir o que é ângulo plano. Ângulo plano é aquele ângulo que comumente desenhamos em nossos desenhos de geometria, é chamado assim, pois é seu nome oficial.
A sua definição oficial é a abertura formada por duas semirretas que se encontram em um ponto. E ele é sempre representado como o na figura abaixo.
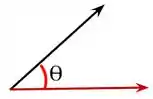
Essa grandeza tem unidade igual a (comprimento/comprimento=1), o que expressa grandeza adimensional. No SI essa unidade pode ser representada pelo radiano e símbolo .
Por exemplo:
Contudo, o SI admite também a unidade grau, de símbolo .
Por exemplo:
Mas essas unidades não são iguais, para converter , temos que saber que:
Passo 2
Agora vamos definir o que é ângulo sólido. Em poucas palavras e mais fácil, ângulo sólido é a projeção do ângulo plano em 3D.
A sua definição oficial é o ângulo com vértice no centro de uma esfera, que subentende na superfície desta esfera uma área medida pelo quadrado do raio da esfera. Geralmente ele é denotado como nos desenhos e figuras.
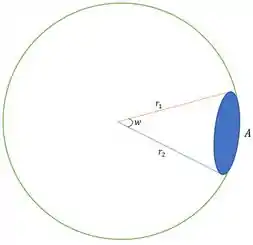
Matematicamente falando, ele é definido como a relação entre a área ( ) do setor desejado e o quadrado do raio ( ).
O ângulo sólido é medido, no SI, em esterorradiano ().
Resposta
Ângulo plano é a abertura formada por duas semirretas que se encontram em um ponto. No SI: e .
Ângulo sólido é o ângulo com vértice no centro de uma esfera. No SI: esterorradiano ().