Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 5.Problemas - Ex. 145

A comporta quadrada AB é mantida na posição mostrada na figura por meio de articulações ao longo de sua aresta superior A e por um pino de cisalhamento em B. Para uma profundidade de água , determine a força exercida sobre a comporta pelo pino de cisalhamento.

Passo 1

Pra começar podemos dividir o carregamento em duas regiões triangulares e calcular as reações em cada uma delas, dessa forma, com o auxílio do diagrama de corpo livre a seguir, temos:

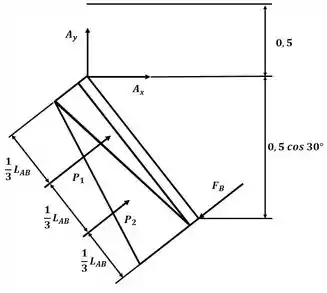
Sabendo que a pressão em um ponto da comporta é dado por:

Onde é o peso específico da água, temos então:

Passo 2

Então agora podemos aplicar o somatório de momento em relação ao ponto para descobrir o valor da força em :

Simplificando o termo que aparece em todos os termos, substituindo os valores de e encontrados no passo 1 e isolando , temos:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma viga é submetida a uma carga distribuída linearmente em ordem decrescente e repousa em dois suportes largos B C e D E , que exercem cargas uniformemente distribuídas para cima como mostrado na fig

117- Quatro vigas, cada qual de comprimento 3 a , são pregadas juntas com um único prego em A , B , C e D . Cada viga é fixada a um suporte localizado a uma distância a a partir da ponta da viga como

118- Quatro vigas, cada qual de comprimento 2 a , são pregadas juntas em seus pontos médios para formar o sistema de suporte mostrado na figura. Considere que apenas forças verticais são exercidas nas

Determine as reações de apoio da viga para a carga dela.

Determine (a) a distância a tal que as reações verticais dos apoios A e B sejam iguais, (b) as reações de apoio correspondentes.