Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 6.Problemas - Ex. 70

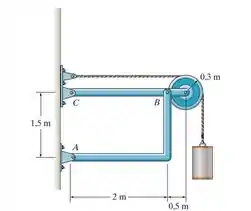
Determine as componentes horizontal e vertical das forças nos pinos B e C . O cilindro suspenso possui massa de 75 kg.

Passo 1

E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!

Devemos determinar as componentes horizontal e vertical das forças nos pinos B e C . Sabemos também que a corda está tracionada com uma força P = 75 ⋅ 9,81 = 735,8   N .

Para obter as componentes dessas forças, vamos analisar apenas a barra C B juntamente da polia. Esboçando o diagrama de corpo livre da nossa estrutura, temos:

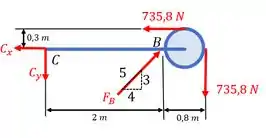
Agora que já temos todas as informações necessárias, vamos as contas!

Passo 2

Agora é a hora de aplicarmos as equações de equilíbrio! Sendo assim, temos:

∑ F x = 0 ∑ F y = 0 ∑ M R C = 0 ⟹ - C x + F B ⋅ 4 5 - 735,8 = 0 - C y + F B ⋅ 3 5 - 735,8 = 0 735,8 ⋅ 0,3 + F B ⋅ 3 5 ⋅ 2 - 735,8 ⋅ 2,8 = 0

Resolvendo o sistema acima obtemos:

F B = 1532,9   N

C x = 491   N

C y = 184   N

E por fim, decompondo a força F B nas componentes horizontal e vertical, temos:

B x = F b ⋅ 4 5 = 1,23   k N

B y = F b ⋅ 3 5 = 920   N

E assim finalizamos a questão!

Resposta

C x = 491   N

C y = 184   N

B x = 1,23   k N

B y = 920   N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A mola tem um comprimento de 0,3 m quando não está esticada. Determine o ângulo θ para o equilíbrio se as hastes uniformes possuem massa de 20k g cada.
Determine a força P no cabo se a mola for comprimida em 0,025m quando o mecanismo está na posição mostrada. A mola tem rigidez k=6k N / m .
A balança de plataforma consiste em uma combinação de alavancas de terceira e primeira classes, de modo que a carga sobre uma alavanca se torna o esforço que move a próxima alavanca. Por meio desse ar
A minicarregadeira tem massa de 1,18 Mg e, na posição mostrada, o centro de massa está em G1. Se houver uma pedra de 300 kg na caçamba, com centro de massa em G2, determine as reações de cada par de r
Determine as componentes horizontal e vertical da reação no pino C.