Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 6.Problemas - Ex. 73
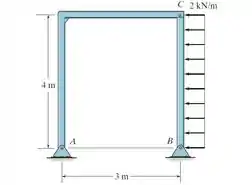
Determine as componentes horizontal e vertical das forças que os pinos e exercem sobre a estrutura.
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!
Devemos determinar as componentes horizontal e vertical das forças que os pinos e exercem sobre a estrutura.
Para conseguirmos obter estes valores, vamos ter que separar a nossa estrutura em duas partes: barra e a barra .
Vamos agora esboçar o diagrama de corpo livre de ambas as barras, a começar pela barra . Ela será:
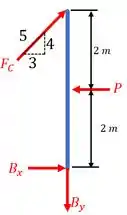
Percebam que o carregamento distribuído foi substituído por uma força pontual no ponto médio do carregamento.
Continuando, para a barra temos:
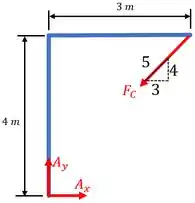
Agora que já temos todas as informações necessárias, vamos as contas!
Passo 2
Agora é a hora de aplicarmos as equações de equilíbrio! Vamos começar analisando a barra . Para ela, temos:
Como , ao resolvermos o sistema acima obtemos:
E assim obtemos as componentes horizontal e vertical da força no pino .
Passo 3
Para finalizarmos a questão, basta analisarmos o diagrama de corpo livre da barra .
Aplicando as equações de equilíbrio, temos:
Resolvendo o sistema acima obtemos:
E assim finalizamos a questão!