Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 6.Problemas - Ex. 109
A mola tem um comprimento de 0,3 m quando não está esticada. Determine o ângulo para o equilíbrio se as hastes uniformes possuem massa de cada.
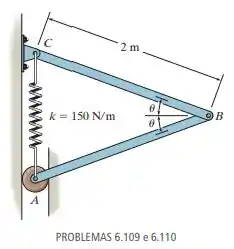
Passo 1
Fala aí, galerinha do Responde aí. Tudo bem? Bora pra mais uma questão.
Primeiramente, se as hastes possuem 20 kg cada, teremos uma força centralizada em cada haste no valor de:
Para que a barra não rotacione:
Agora, podemos determinar o comprimento total da mola. Como o encontrado diz respeito apenas a segunda parte da barra ,sabemos que ele será:
Agora, temos os 3 lados do triângulo formado. Pela lei dos cossenos:
Resposta
Exercícios de Livros Relacionados
A viga composta está engastada em A e apoiada por balancins em B e C. Existem dobradiças (pinos) em D e E. Determine as reações nos apoios.
A estrutura está sujeita aos carregamentos mostrados. O membro AB é sustentado por uma junta esférica em A e uma luva em B. O membro CD é sustentado por um pino em C. Determine as componentes x, y, z
O guindaste de pilar está sujeito à carga com massa de 500 kg. Determine a força desenvolvida na haste de ligação AB e as reações horizontal e vertical no suporte com pino C quando a lança está presa
A mola tem um comprimento de 0,3 m quando não está esticada. Determine a massa m de cada haste uniforme se cada ângulo vale 30 ° para haver equilíbrio.
A viga composta está apoiada por pino em B e por balancins em A e C. Há uma dobradiça (pino) em D. Determine as reações nos apoios.