Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 6.Problemas - Ex. 72
Determine as componentes horizontal e vertical das forças nos pinos e .
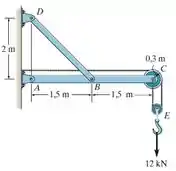
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!
Esta é uma questão bem tranquila. Apesar de ter esta relação com polias e com a corda, vocês verão que a chave da questão está no diagrama de corpo livre, de como vamos desenhá-lo.
Então vejamos, o objetivo desta questão é obtermos as componentes horizontal e vertical das forças nos pinos e . Para as forças no pino , basta utilizarmos o método dos nós para este ponto.
Agora, para as forças em , vamos começar esboçando o diagrama de corpo livre na barra . Sendo assim, temos:
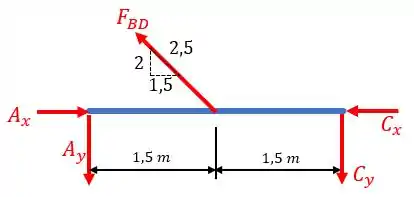
Eita! Só tem incógnitas ai no meio! Mas calma, muita calma. As reações em devido a polia podem ser facilmente identificadas, basta apenas que façamos o diagrama de corpo livre para as polias. Desta forma, temos:
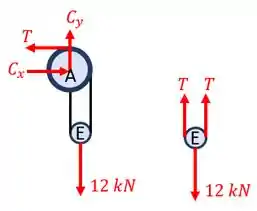
Agora sim já temos informações suficientes para começarmos a questão! Então, vamos as contas!
Passo 2
Para que a gente consiga determinar as reações em , vamos ter que determinar antes quem são , e . Logo, vamos trabalhar com o diagrama de corpo livre das polias.
Começando pela polia , como ela está em equilíbrio, temos:
Analisando agora o diagrama de corpo livre das duas polias simultaneamente, temos:
Passo 3
Após a determinação das reações em , vamos determinar as reações em .
Como a barra está em equilíbrio, temos:
Resolvendo o sistema acima obtemos:
E assim finalizamos a primeira parte da questão!
Passo 4
Para que a gente possa concluir em si a questão, vamos calcular as componentes da reação em .
Esboçando o diagrama de equilíbrio em torno deste ponto, temos:
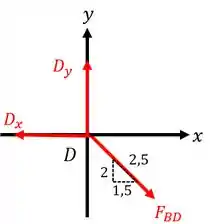
Aplicando as equações de equilíbrio, obtemos:
E assim finalizamos a questão!