Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 6.Problemas fundamentais - Ex. 18

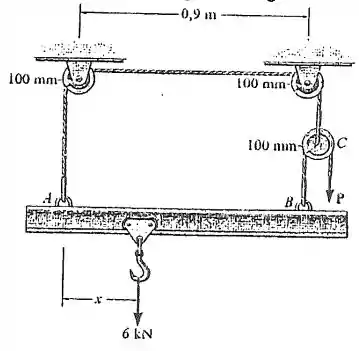
Determine a força P necessária para suspender o peso. Além disso, determine o posicionamento x correto do gancho para o equilíbrio. Despreze o peso da viga.

Passo 1

A fim de determinar a força para suspender se vê necessário fazer o diagrama de corpo livre da polia C e da viga (pois são nelas que a força P mais tem influência) e analisar as forças exercendo em seus corpos. Assim, relacionando as forças que atuam nelas será possível encontrar o resultado desejado.

Passo 2

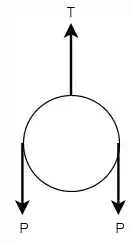
Logo, fazendo o DCL da polia C tem-se:

Passo 3

Agora, com o DCL da polia é possível determinar a equação do equilíbrio de forças atuando nela.

Então, como há apenas forças verticais, será feito o somatório de forças no eixo y tal que:

∑ F y = 0 ⇒ T - 2 P = 0

T = 2 P   1

Passo 4

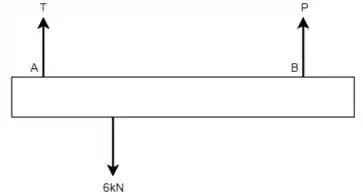
Da mesma forma, fazendo o DCL da viga:

Passo 5

Novamente, com o DCL se torna possível montar a equação de equilíbrio no eixo y da viga que será dada por:

∑ F y = 0 ⇒ T + P - 6 = 0

Podemos substituir 1 nesta equação tal que:

2 P + P - 6 = 0 ⇒ 3 P = 6

P = 2   k N

Passo 6

Agora, com o valor da força P e aplicando o princípio dos momentos em relação ao ponto A se torna possível determinar o valor do posicionamento do gancho.

Logo, considerando que o momento será positivo no sentido anti-horário:

∑ M A = 0 ⇒ P 0,9 + 0,1 - 6 x = 0

x = P 6 = 2 6

x = 0,333 m

Resposta

P = 2   k N

x = 0,333 m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Identifique os membros de força zero na treliça.
Determine a maior carga P que pode ser aplicado na treliça de modo que nenhum dos membros esteja sujeito a uma força excedendo 2 k N em tração ou 1,5 k N em compressão.
Determine as forças nos membros F D e D B da estrutura. Além disso, encontre as componentes horizontal e vertical da reação que o pino em C exerce sobre o membro A B C e o membro E D C .
O dispositivo de elevação consiste em dois conjuntos de membros cruzados e dois cilindros hidráulicos, DE, localizados simetricamente em cada lado da plataforma. A plataforma possui massa uniforme de
A prensa está sujeita a uma força F no punho. Determine a força de prensagem vertical atuando em E .