Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 6.Problemas - Ex. 71
Determine a maior força que pode ser aplicada à estrutura se a maior força resultante que atua em puder ter uma intensidade de .
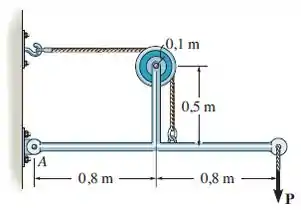
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!
Esta é uma questão bem tranquila. Apesar de ter esta relação com polias e com a corda, vocês verão que a chave da questão está no diagrama de corpo livre, de como vamos desenhá-lo.
Então vejamos, como o nosso objetivo é obter a força resultante em , temos que escrever um diagrama que apresente apenas 3 componentes de forças distintas (sendo 2 em , dado por e ).
Para que a gente consiga isto, basta tirar substituir o vínculo em e na corda tracionada acima pelas suas forças. Sendo assim, teremos o seguinte diagrama de corpo livre:
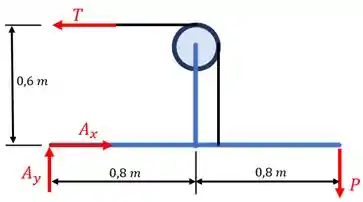
Agora que a gente já sabe o que fazer, vamos as contas!
Passo 2
Vamos começar determinando as componentes horizontal e vertical da força em . Para isto, vamos utilizar as equações de equilíbrio.
Portanto,
Resolvendo o sistema obtemos que:
Então, a força resultante em será:
Então, como queremos obter o maior valor de tal que a força máxima atuante em seja , temos:
E assim finalizamos a questão!