Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 6.Problemas fundamentais - Ex. 24

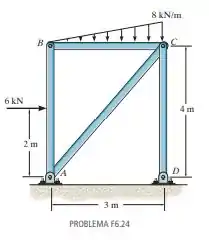
Determine as componentes da reação em D e as componentes da reação que o pino em A exerce sobre o membro BA.

Passo 1

Fala aí, galerinha do Responde aí. Tudo bem? Bora pra mais uma questão.

Vamos começar fazendo o nosso D.C.L, no membro livre AB

Passo 2

Pela figura

tan ⁡ θ = 4 3

θ = tan - 1 ⁡ 4 3

θ = 53.13 °

Tomemos momentos sobre A

∑ M A = 0

B x 4 - 6 2 = 0

B x = 12 4

B x = 3   k N

Onde B x é a força de reação horizontal no ponto B.

Aplique a equação de equilíbrio na direção horizontal.

∑ F x = 0

A x - F A C cos ⁡ 53.13 = 0

A x = F A C cos ⁡ 53.13 °                 ( 1 )

Passo 3

Aplicaremos a equação de equilíbrio na direção vertical

∑ F y = 0

A y - B y = 0             2

Onde, A y e B y são reações verticais no ponto A e B, respectivamente.

Passo 4

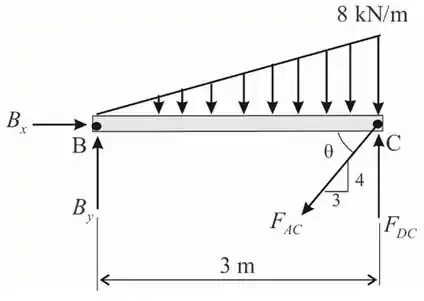
Vamos desenhar o nosso D.C.L na barra BC

Passo 5

Tomemos momento sobre C

∑ M C = 0

- B y 3 + 1 2 × 8 × 3 3 3 = 0

B y = 12 3

B y = 4   k N

Aplicaremos a equação de equilíbrio na direção vertical.

∑ F y = 0

B y - F A C sin ⁡ 53.13 + F D C - 1 2 × 8 × 3 = 0

4 - F A C sin ⁡ 53.13 + F D C - 1 2 × 8 × 3 = 0

F A C sin ⁡ 53.13 - F D C = - 8

Vamos aplicar a equação de equilíbrio na direção horizontal

∑ F x = 0

B x - F A C cos ⁡ θ = 0

F A C = 3 cos ⁡ 53.13 °

F A C = 5   k N  

Passo 6

Vamos fazer a substituição numérica na equação (30

5 sin ⁡ 53.13 ° - F D C = - 8

F D C = 5 sin ⁡ 53.13 ° + 8

F D C = 12   k N

Passo 7

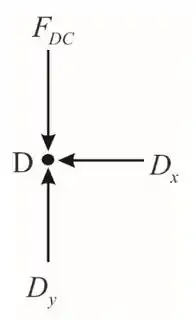
Vamos desenhar o nosso D.C.L no nó D

Passo 8

Aplicaremos a equação de equilíbrio na direção horizantal

∑ F x = 0

D x = 0

Onde, D x é a força de reação horizontal no nó D

Portanto, a componente horizontal de reação em D é 0   k N .

Aplicando equaçãode equilíbrio na direção vertical

∑ F y = 0

D y - F D C = 0

D y - F D C = 0

D y = 12   k N

Portanto, o componente vertical da reação em D é 12   k N ↑

A x = 5 cos ⁡ 53.13 °

A x = 6   k N

Portanto, a compente horizontal da reação em A é 6   k N .

A y - 4 = 0

A y = 4   k N

Portanto, a componente vertical da reação em A é 0   k N .

Resposta

D y = 12   k N

D x = 0   k N

A y = 4   k N

A x = 3   k N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A mola tem um comprimento de 0,3 m quando não está esticada. Determine o ângulo θ para o equilíbrio se as hastes uniformes possuem massa de 20k g cada.
Determine a força P no cabo se a mola for comprimida em 0,025m quando o mecanismo está na posição mostrada. A mola tem rigidez k=6k N / m .
A balança de plataforma consiste em uma combinação de alavancas de terceira e primeira classes, de modo que a carga sobre uma alavanca se torna o esforço que move a próxima alavanca. Por meio desse ar
A minicarregadeira tem massa de 1,18 Mg e, na posição mostrada, o centro de massa está em G1. Se houver uma pedra de 300 kg na caçamba, com centro de massa em G2, determine as reações de cada par de r
Determine as componentes horizontal e vertical da reação no pino C.