Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 5.Problemas - Ex. 225
Determine as coordenadas do centro de massa do corpo construído em chapa de aço e uma barra de aço. A espessura da placa é de 2 mm. O diâmetro da haste é de 4 mm e seu comprimento é de 50 mm. A origem O está na espessura média da placa, e a haste é soldada à face da placa. Qual é a massa do corpo?
Passo 1
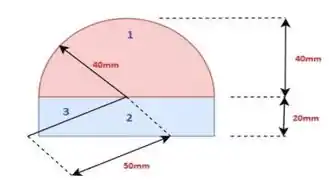
O corpo composto pode ser subdividido em 3 partes diferentes, conforme mostrado na figura.
Por inspeção, fica claro que, por simetria, a coordenada y do centro de massa de cada uma das partes subdivididas é zero.
Passo 2
A massa de cada peça pode ser calculada obtendo o volume e multiplicando-o pela densidade do aço .
Parte 1
Parte 2
Parte 3
Passo 3
Por inspeção, podemos obter as coordenadas x, z de cada parte. Usando a fórmula , podemos obter a coordenada z da Parte 1.
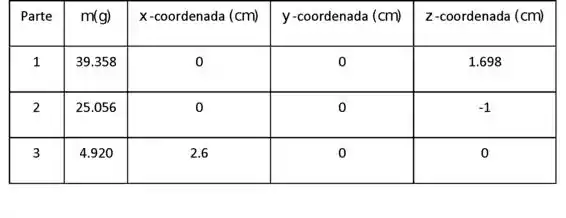
Passo 4
Massa total do corpo
As coordenadas do centro de massa podem ser obtidas usando a equação (5/7) a partir do princípio dos momentos: