Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 6.Problemas - Ex. 145

O invólucro semicilíndrico de massa me raio r é enrolado através de um ângulo θ pela força P que permanece tangente à sua periferia em A, como mostrado. Se P for aumentado lentamente, plote o ângulo de inclinação θ como uma função de P até o ponto de escorregamento. Determine o ângulo de inclinação θmax e o valor correspondente Pmax para o qual ocorre o escorregamento. O coeficiente de atrito estático é de 0,30

Passo 1

Primeiro, vamos desenhar o diagrama de corpo livre

Uma vez que conhecemos a expressão do centro do arco, podemos calcular a distância l

l = 2 r π

Uma vez que a força F A é máxima força de fricção, escreveremos como

F A = μ s ⋅ N A (1)

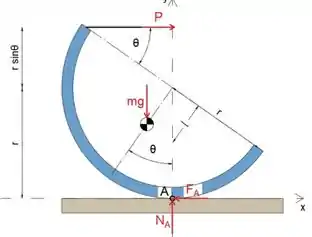
Passo 2

Equacionando a soma dos momentos sobre o ponto A a zero. vamos determinar a força P

∑ A     = 0 ( r + r s i n ⁡ θ ) P - l s i n ⁡ θ ⋅ m g = 0 P = l s i n ⁡ θ ⋅ m g r + r s i n ⁡ θ

Substituiremos l por 2 r π

P = 2 r π s i n ⁡ θ ⋅ m g r ( 1 + s i n ⁡ θ ) P = 2 s i n ⁡ θ π ( 1 + s i n ⁡ θ ) m g (2)

Passo 3

Equacionando a soma das forças na direção x - e y - a zero, podemos determinar as forças de reação FA e NA

∑   F y   = 0   - m g + N A = 0 N A = m g ∑   F x   = 0   - F A + P = 0 F A = P

Substituiremos F A e P pelas expressões ( 1 ) e ( 2 ) respectivamente

μ s ⋅ N A = 2 s i n ⁡ θ π ( 1 + s i n ⁡ θ ) m g

Podemos substituir N A por m g

μ n ⋅ m g = 2 s i n ⁡ θ π ( 1 + s i n ⁡ θ ) m g   / ⋅ 1 m g

Dividiremos ambos lados da equação por m g para ter:

μ s = 2 s i n ⁡ θ π ( 1 + s i n ⁡ θ ) (3)

Passo 4

Agora tudo o que temos a fazer é expressar o ângulo θ da expressão acima

μ s = 2 s i n ⁡ θ π ( 1 + s i n ⁡ θ ) μ s + π ( 1 + s i n ⁡ θ ) = 2 s i n ⁡ θ μ s ⋅ π + μ s + π s i n ⁡ θ = 2 s i n ⁡ θ μ s = π = 2 s i n ⁡ θ - μ s ⋅ π s i n ⁡ θ μ s ⋅ π = 2 - μ s ⋅ π s i n ⁡ θ s i n ⁡ θ = μ s + π 2 - μ s ⋅ π θ = a r c s i n ⁡ μ s ⋅ π 2 - μ n ⋅ π

Substituiremos θ por 90 ∘ na expressão (3) para ter o requerido valor de μ s

μ s 90 ∘ = 2 s i n ⁡ 90 ∘ π 1 + s i n ⁡ 90 ∘

μ s 90 ∘ = 0.3183

Resposta

θ = a r c s i n ⁡ μ s ⋅ π 2 - μ n + π μ s 90 . = 0.3183

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Grampos de placa para serviço pesado com cames de cunha são projetados para ser usado em pares para levantar e transportar grandes placas de aço. À medida que cada came começa a fazer efeito, a placa
Um carrinho de mão carregado é colocado em uma inclinação acidentada. O peso combinado do carrinho de mão e sua carga atua no centro de gravidade G. (a) Determine o ângulo máximo θ para o qual o carri
O corpo homogêneo com dois pés pequenos e duas rodas ideais estão em repouso na inclinação acidentada. (a) Suponha sem derrapagem e determine o valor máximo do ângulo θ para o qual o corpo não vira em
Um carpinteiro de 100k g se agacha sobre uma folha de 18k g de contraplacado quando ele está prestes a efetuar um conserto de telhas. Determine a força de atrito que a superfície do telhado exerce sob
Repita o Prob. 6 / 28 , mas agora o carro tem roda dianteira.