Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 7.Problemas - Ex. 144

Determine a deformação específica ϵ x utilizando a roseta mostrada sabendo que foram verificadas as seguintes deformações:

ϵ 1 = + 480   μ                       ϵ 2 = - 120   μ                       ϵ 3 = + 80   μ

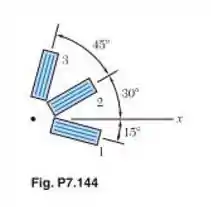
Passo 1

Opaa! Fala pessoal, beleza? Bora pra mais um?! Para resolver esse exercício, vamos utilizar o conjunto de equações 7.60, dado por:

ϵ 1 = ϵ x cos 2 ⁡ θ 1 + ϵ y s e n 2   θ 1 + γ x y s e n   θ 1 cos ⁡ θ 1

ϵ 2 = ϵ x cos 2 ⁡ θ 2 + ϵ y s e n 2   θ 2 + γ x y s e n   θ 2 cos ⁡ θ 2

ϵ 3 = ϵ x cos 2 ⁡ θ 3 + ϵ y s e n 2 θ y + γ x y s e n   θ 3 cos ⁡ θ 3

Vamos substituir os valores conhecidos para cada um dos 3 casos descritos, chegando num sistema de equações, depois disso temos que resolver o sistema. Então bora lá.

Passo 2

Tá legal! Vamos começar escrevendo os ângulos θ que nós temos:

θ 1 = - 15 °

θ 2 = 30 °

θ 3 = 75 °

Então beleza! Vamos substituir os valores conhecidos na primeira equação, chegando em:

480 = ϵ x cos 2 ⁡ ( - 15 ° ) + ϵ y s e n 2 - 15 ° + γ x y s e n - 15 ° c o s ⁡ ( - 15 ° )

480 = 0,933 ϵ x + 0,06699 ϵ y - 0,25 γ x y

Essa será nossa equação 1. Agora vamos substituir os valores conhecidos na segunda equação, chegando em:

- 120 = ϵ x cos 2 ⁡ ( 30 ° ) + ϵ y s e n 2 30 ° + γ x y s e n 30 ° c o s ⁡ ( 30 ° )

- 120 = 0,75 ϵ x + 0 , 2 5 ϵ y + 0,433 γ x y

Essa será nossa equação 2. E agora, substituindo os valores conhecidos na terceira equação, chegamos em:

80 = ϵ x cos 2 ⁡ ( 75 ° ) + ϵ y s e n 2 75 ° + γ x y s e n 75 ° c o s ⁡ ( 75 ° )

80 = 0,06699 ϵ x + 0,933 ϵ y + 0,25 γ x y

E essa será nossa equação 3.

Passo 3

Então, com uma calculadora boa em mãos ou resolvendo esse sistema linear em alguma programinha, chegamos em:

ϵ x = 253   μ

ϵ y = 307   μ

γ x y = - 893   μ

E, a nossa deformação pedida no enunciado foi ϵ x , ou seja, nossa resposta será:

ϵ x = 253   μ

Shooow! Fechamos mais um exercício, valeeu!

Resposta

ϵ x = 253   μ

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Sabe-se que existe um estado plano de deformação na superfície de um componente de máquina. Sabendo que E = 200 GPa e G = 77,2 GPa, determine a direção e a intensidade das três deformações específicas
Resolva o Problema 7.154 considerando que o extensômetro forma um ângulo β = 35 ° com um plano horizontal.
Resolva o Problema 7.152 considerando que o extensômetro forma um ângulo β = 35 ° com uma linha paralela ao centro do eixo.
O seguinte estado de deformação foi determinado na superfície de uma peça de máquina de ferro fundido: ϵ x = - 720μ ; ϵ y = - 400μ ; γ x y = 660μ Sabendo que E = 69 GPa e G = 28 GPa, determine os plan
O seguinte estado de deformação dado foi medido na superfície de uma placa fina. Sabendo que a superfície da placa está livre de tensão, determine ( a ) a direção e a intensidade das deformações princ