Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 7.Problemas - Ex. 155

Resolva o Problema 7.154 considerando que o extensômetro forma um ângulo β = 35 ° com um plano horizontal.

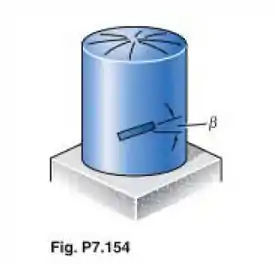
Passo 1

Opaa! Fala pessoal, beleza? Bora pra mais um?! Para resolver esse exercício, vamos precisar utilizar a equação para a tensão gerada pela pressão no tanque na direção x, que é dada por:

σ x = p r t

Em que p é a pressão manométrica, r é o raio interno e t é a espessura da parede. Sabemos também que a tensão gerada na direção y para os vasos de parede fina é metade da tensão em x, então temos:

σ y = p r 2 t = σ x 2

Vamos utilizar essas equações para escrever as deformações nas direções x e y. Com esses valores poderemos desenhar o círculo de Mohr para o nosso caso e depois rotacionar ele de um ângulo β para utilizar a leitura fornecida pelo extensômetro. Fazendo isso conseguimos encontrar o valor da pressão pedido no enunciado, então bora lá!

Passo 2

Tá legal, já vimos as expressões para as tensões nas direções x e y no passo 1, agora, sabendo que as deformações nessas direções são dadas por:

ϵ x = σ x - ν σ y E

ϵ y = σ y - ν σ x E

Substituindo as expressões conhecidas, deixando em função de σ x , teremos:

ϵ x = σ x - 0,3 σ x 2 E → ϵ x = 0,85 σ x E

ϵ y = σ x 2 - 0,3 σ x E → ϵ y = 0,2 σ x E

No nosso caso não temos tensão de cisalhamento, então a deformação de cisalhamento será:

γ x y = 0

Com esses pontos já podemos desenhar nosso círculo de Mohr, que será dado por:

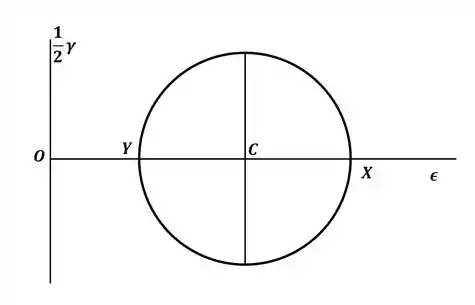
Passo 3

Agora, com o círculo de Mohr, vamos encontrar a expressão da deformação média, que será dada por:

ϵ m e d = ϵ x + ϵ y 2

Substituindo as expressões encontradas no passo 2, teremos:

ϵ m e d = 0,85 σ x E + 0,2 σ x E 2 → ϵ m e d = 0,525 σ x E

E, o nosso raio do círculo será dado por:

R = ϵ x - ϵ y 2 = 0,85 σ x E - 0,2 σ x E 2 → R = 0,325 σ x E

Agora, nós vamos rotacionar o ponto X de um ângulo β no elemento diferencial, ou seja, rotacionar o círculo de Mohr de 2 β , então teremos:

Então, para esse ponto, teremos a deformação em x igual a:

ϵ x ' = ϵ m e d + R c o s   2 β

Substituindo as expressões conhecidas, chegaremos em:

ϵ x ' = 0,525 σ x E + 0,325 σ x E cos ⁡ 2 β = σ x E 0,525 + 0,325 cos ⁡ 2 β

E, isolando a tensão em x dessa expressão, teremos:

σ x = E ϵ x ' 0,525 + 0,325 cos ⁡ 2 β

Passo 4

Agora vamos utilizar a equação para a tensão normal na direção x que vimos lá no passo 1:

σ x = p r t

Isolando a pressão dessa equação, teremos:

p = σ x t r

Agora, substituindo a expressão obtida para σ x no passo 3 e substituindo os valores conhecidos, chegamos em:

p = E ϵ x ' t 0,525 + 0,325 cos ⁡ 2 β r = 200.10 9 280.10 - 6 0,006 0,525 + 0,325 cos ⁡ 70 ° 0,3

p = 1,76   M P a

Feshooow!

Resposta

p = 1,76   M P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para o estado de tensões dado, determine as tensões normal e de cisalhamento depois que o elemento mostrado sofreu uma rotação de (a) 25 ° no sentido horário e (b) 10 ° no sentido anti-horário.
Determine o intervalo de valores de σ x para o qual a tensão de cisalhamento máxima no plano das tensões é igual ou menor que 69M P a .
Para o estado plano de tensão mostrado, determine o maior valor de σ y para o qual a tensão de cisalhamento máxima no plano das tensões é igual ou menor que 75M P a .
As fibras de um elemento de madeira formam um ângulo de 15 ° com a vertical. Para o estado de tensão mostrado, determine (a) a tensão de cisalhamento no plano da tensão paralela às fibras e (b) a tens
Para o estado de tensões dado, determine as tensões normal e de cisalhamento depois que o elemento mostrado sofreu uma rotação de (a) 25 ° no sentido horário e (b) 10 ° no sentido anti-horário.