Resolva o Problema 8,45 considerando que h =304,8mm
Passo 1
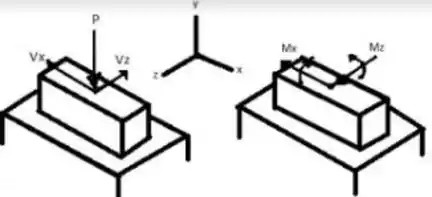 Calcule as forças e duplas na seção contando a, b, e c, temos o esboço abaixo :D
Calcule as forças e duplas na seção contando a, b, e c, temos o esboço abaixo :D
Sendo temos que calcular os momentos e a inércia respectivamente :D
Passo 2
A tensão é dada por:
- Ponto a:
- Ponto b:
- Ponto c:
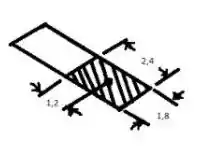
Passo 3

Passo 4
Resposta
- 0