Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 7.Problemas - Ex. 51
Determine os diagramas de esforço cortante e de momento fletor para a viga.
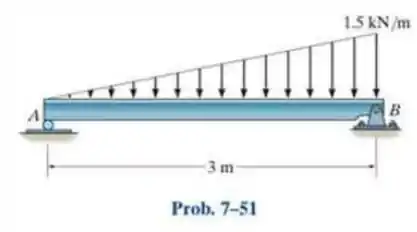
Passo 1
O problema quer que encontremos o esforço cortante e o momento fletor. E o primeiro passo pra fazer isso é encontrar as reações nos apoios A e B. Então observando rapidamente, podemos notar que o corpo encontra-se em equilíbrio, então a gente vai usar a equação de equilíbrio, pois a soma das forças e dos momentos são .
Então lembra que essa carga distribuída triangular é equivalente a uma carga pontual com valor igual a área desse triângulo que a carga distribuída ocupa, ou seja 15 x 3/2. E o centroide dele vai ser em 2/3 da base, ou seja distância de 2m do ponto A. (Cuidado! Que se a carga distribuída fosse triangular mas decrescente, o centroide seria 1/3 da base. Mas isso é outro caso.)
Daí o somatório de momentos no ponto A, vai dar pra gente a reação em B.
E pra achar a reação em A, vamos fazer o somatório de forças verticais.
Passo 2
Agora que temos as reações nos apoios, o jeito de resolver esse tipo de problema é calcular os diagramas de esforços é fazer cortes na nossa viga. Vamos fazer um corte cortando a carga distribuída, num ponto que fique a uma distância x a direita do apoio A. E nesse ponto corte (vamos chamar de ponto C) vai ter um esforço cortante V e um momento fletor M. Os 2 aparecem ali a direita no diagrama de corpo livre abaixo.
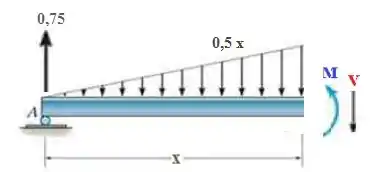
Agora, pra achar a equação pro momento fletor, vamos fazer o somatório de momentos no ponto de corte. O sentido anti-horário é o positivo. Cuidado! Dessa vez o braço de alavanca da carga distribuída vai ficar 1/3 da base x, porque estamos fazendo o somatório de momentos a direita.
Agora pra achar o cortante, vamos fazer o somatório de forças veticais:
Perfeito! Agora é só traçar os diagramas!
Passo 3
Pra definir o diagrama, é a própria função. As vezes a gente já sabe só de olhar. Mas as vezes a gente precisa substituir alguns valores de x pra entender como vai ficar o formato e aí poder traçar. Principalmente quando tem descontinuidades.
O esforço cortante vai ficar assim:
O momento fletor é uma função do terceiro grau e vai ficar com essa cara:
É sempre bom colocar no diagrama esses pontos principais, como valores máximos e mínimos e os contornos.
Resposta
