Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 7.Problemas - Ex. 66

Determine os diagramas de esforço cortante e de momento fletor para a viga de dupla extremidade em balanço.

Passo 1

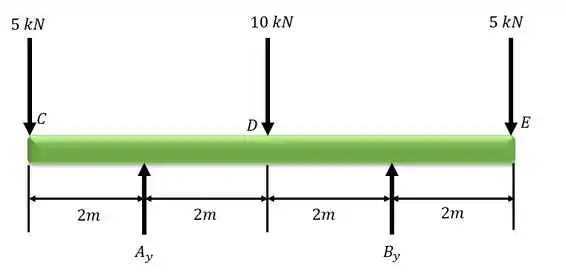
Desenhando o diagrama do corpo livre do corpo:

Passo 2

Com o diagrama do corpo livre traçado, podemos calcular as reações de apoio: Σ F y = 0 A y + B y = 5 + 10 + 5 A y = 20 - B y

Σ M A = 0 4 B y =   - 5 × 2 + 10 × 2 + 5 × 6   B y = 10   k N

Portanto:

A y = 20 - B y = 20 - 10 A y = 10   k N

Passo 3

Vamos começar pelo trecho CA ( 0 < 2 ) :

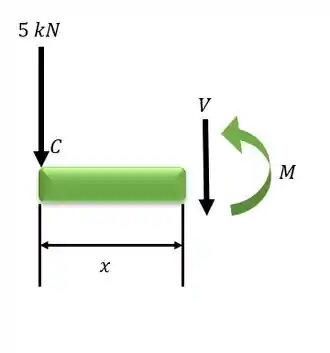
Aplicando a condição de equilíbrio de forças no eixo y:

Σ F y = 0 5 + V = 0 V = - 5   k N

Aplicando a condição de equilíbrio em relação ao momento em relação ao ponto A:

Σ M A = 0 M = A y ⋅ x M = - 5 x   k N ⋅ m

Passo 4

Trecho CD( 0 ≤ x < 4 ):

Σ F y = 0 5 - A y + V = 0 V = A y - 5 = 10 - 5 V = 5   k N

M = V × x   - A y × 2 M = 5 x - 20   k N ⋅ m

Passo 5

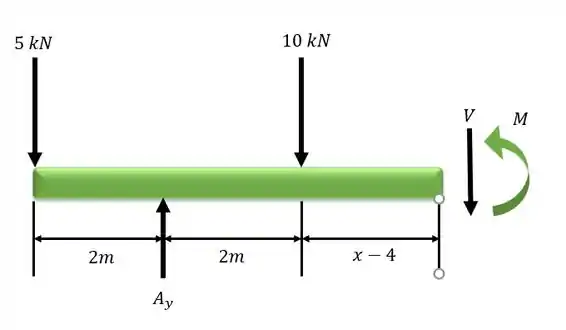
Trecho CD( 0 ≤ x < 6 ):

Σ F y = 0 5 - A y + 10 + V = 0 V = - 5 + 10 - 10 V = - 5   k N

M = V × x   - A y × 2 + 10 × 4 M = - 5 x - 10 × 2 + 40 M = - 5 x + 20   k N ⋅ m

Passo 6

Trecho CD( 0 ≤ x < 8 ):

Σ F y = 0 5 - A y + 10 - B y + V = 0 V = - 5 + A y - 10 + B y V = - 5 + 10 - 10 + 10 V = 5   k N

M = 5 ⋅ x - B y × 6 + 10 × 4 - A y × 2   M = 5 x - 10 × 6 + 10 × 4 - 10 × 2 M = 5 x - 40   k N ⋅ m

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine os diagramas de esforço cortante e de momento fletor para a viga com extremidade em balanço.
O eixo está apoiado em um mancal axial liso em A e um mancal radial liso em B. Determine os diagramas de esforço cortante e de momento fletor para o eixo.
Determine os diagramas de esforço cortante e de momento fletor para a viga.
O eixo está apoiado por um mancal axial liso em A e um mancal radial liso em B . Determine os diagramas de esforço cortante e de momento fletor para o eixo.
Determine os diagramas de esforço cortante e de momento fletor para a viga.