Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 7.Problemas - Ex. 74
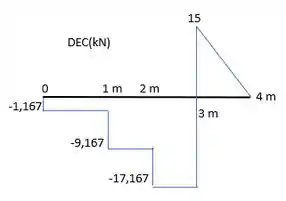
Determine os diagramas de esforço cortante e de momento fletor para a viga.
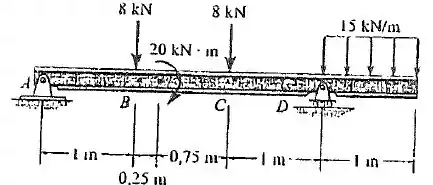
Passo 1
O problema quer que a gente encontre o diagrma do esforço cortante e o momento fletor na viga. Nesse tipo de questão a gente segue um passo a passo maneiro e dá bom!
Vamos começar calculando as reações no ponto e , para isso vamos considerar como o eixo de rotação e o sentido anti-horário como positivo
Lembrando que a viga está em equilíbrio, a soma das forças fica:
Lindo!
Passo 2
Se a gente fosse tentar achar as equações de e para essa viga ia dar muitooo trabalho. Então o que a gente vai fazer é usar um método gráfico. Uhul!
Como ele funciona para o cortante? Vou te mostrar. Temos essa viga:
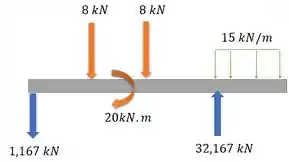
A ideia é a gente seguir essas setinhas para desenhar nosso diagrama e ignorar o momento concentrado, já que estamos no diagrama do cortante.
Fica assim:
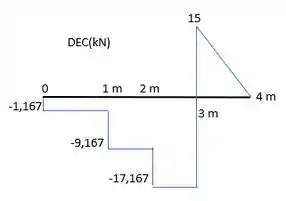
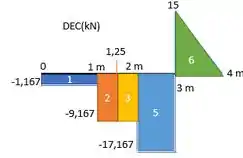
Como a gente fez: Aí nessa reação em , a gente desce , fica constante até a força de , desce esse valor, fica constante até o próximo , nesse ponto a gente desce esse valor de novo e fica constante até .
Aí aqui temos que ter cuidado. Temos a reação. Então a gente dá um pulo para cima de . Só que nesse ponto já começa a carga distruibuida de . Aí a gente faz uma reta descendo com inclinação de (a partir do ponto onde paramos em , depois do pulo) até chegar ao final da viga.
Para confirmar se está certo, esse final tem que ser zero. Como ficou ali na nossa 😊
Passo 3
Também podemos usar um método gráfico para o momento fletor. A ideia é que o momento em cada ponto é a soma algébrica da área no diagrama cortante.
Só temos que tomar cuidado com o momento concentrado. No ponto que ele está, como ele está no sentido horário, há um pulo para cima no diagrama. Então a partir desse ponto, os momentos serão a soma algébrica das áreas do diagrama cortante até o ponto em questão mais esse momento.
Vamos calcular as áreas. Lembra que agora o momento é um ponto importante, por isso a gente calcula área antes e depois dele.
Aí os momentos ficam:
A partir de , a gente adiciona o momento concentrado, aí a gente precisa calcular esse ponto com o momento e um ponto auxiliar sem o momento.
Entre as cargas pontuais, ligamos esses pontos por retas. Já entre e , ligamos os pontos por uma parábola, com concavidade para baixo, já que nesse intervalo é descrescente.
Fica assim:
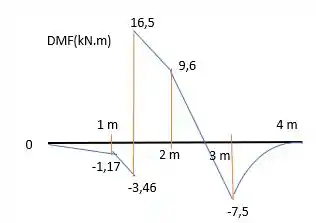
Resposta
