Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 7.Problemas - Ex. 66
Determine a força normal, a força cortante e o momento fletor no elemento curvo em função de u, onde .
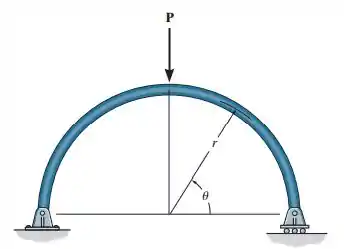
Passo 1
Fala, galera do RespondeAí. Tudo beleza? Bora para mais um exercício de Mecânica. Para esta viga composta vamos primeiro utilizar a semelhança de triângulos a fim de determinarmos a altura do triângulo menor de base . Vamos de chamar essa altura de , temos que:
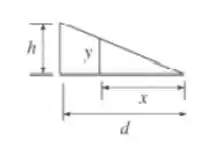
Logo,
Passo 2
Em seguida, vamos utilizar o peso específico que nos foi dado. Sabemos que a força peso é dada por:
Então, vamos calcular a força cortante e o momento fletor. Para isso, vamos analisar o que acontece quando fazemos um corte transversal na viga. Pelo DCL, temos:
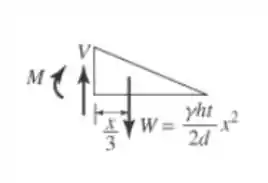
Com isso, vamos determinar o a força cortante e o momento fletor...
Pelo somatório das forças no eixo , temos:
E também, considerando o momento positivo girando no sentido anti-horário, vamos fazer o somatório dos momentos:
Opa, é isso, galera. Bora praticar mais!!!