Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 7.Problemas - Ex. 63
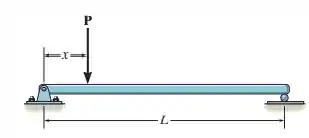
A viga falhará quando o momento fletor máximo for . Determine a posição da força concentrada e sua menor intensidade que causará a falha.
Passo 1
Fala, galera do RespondeAí. Beleza? Bora para mais um exercício de Mecânica. Neste problema, devemos determinar a posição da força concentrada e sua menor intensidade que causará a falha, que ocorre quando momento fletor for máximo.
Sabemos que o momento fletor máximo ocorre na posição em que a carga atua, ou seja:
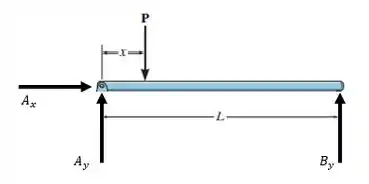
Portanto, devemos determinar os momentos fletores desta viga. Para isso, vamos começar esboçando o DCL:
Passo 2
Em seguida, vamos utilizar a equação de momento no ponto para determinarmos a reação no apoio , temos:
E pelas equações de equilíbrio, vamos determinar as demais reações nos apoios. Pelo somatório das forças no eixo , temos:
E para o eixo , temos:
Passo 3
Então, vamos calcular o momento fletor. Para isso, vamos analisar o que acontece quando fazemos um corte transversal na viga. Primeiro, para a porção da viga. Podemos esboçar esse DCL assim:
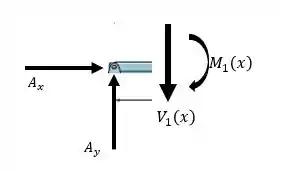
Com isso, vamos determinar o momento fletor...
Considerando o momento positivo girando no sentido anti-horário, vamos fazer o somatório dos momentos:
Passo 4
Para a segunda porção da viga, ou seja, , temos:
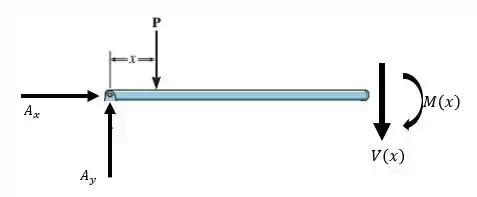
Então, temos que o momento fletor vai ser:
Com isso, podemos determinar o momento máximo, sabemos que onde ele ocorre pois definimos no Passo 1. em . Logo:
Podemos derivar esta equação, temos:
Agora que encontramos a posição em que o momento máximo ocorre, basta substituirmos em uma das equações de momento fletor a fim de determinarmos a carga . Fica assim:
Opa, é isso, galera. Bora praticar mais!!!