Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 8.Problemas - Ex. 140
O cilindro está sujeito a uma carga que tem um peso . Se o coeficiente de resistência ao rolamento para as superfícies superior e inferior do cilindro forem e , respectivamente, mostre que uma força horizontal de intensidade de é necessáia para mover a carga e, portanto, rolar o cilindro para frente. Despreze o peso do cilindro.
Passo 1
Galera, quando um cilindro rígido rola com velocidade constante por uma superfície rígida, a força normal exercida pela superfície sobre o cilindro atua perpendicularmente ao ponto de contato. Mas nós sabemos que nenhum material é perfeitamente rígido e, portanto, a reação da superfície sobre o cilindro consiste em uma distribuição de pressão normal. Conforme ele rola, o material da superfície na frente do cilindro retarda o movimento, pois ele está sendo deformado. Para manter esse movimento constante, é necessária uma força motriz horizontal ser aplicada no cilindro.
Para manter o cilindro em equilíbrio, ou seja, manter ele rolando a uma velocidade constante é preciso que seja concorrente com a força motriz e o peso . Assim, temos a seguinte expressão para esse tipo de situação:
Passo 2
Para começar a resolução dessa questão, vamos desenhar o diagrama de corpo livre para essa situação!
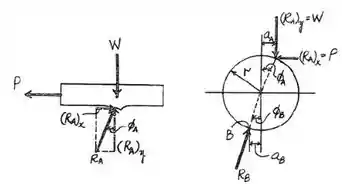
Passo 3
Vamos começar analisando o primeiro diagrama de corpo livre (esquerda). Usando os eixos x vamos calcular o somatório das forças verticais e horizontais que, num sistema em equilíbrio, devem ser iguais a zero. Assim,
Passo 4
Para um corpo em equilíbrio, o somátio dos momentos em relação a um ponto deve ser igual a zero. Vamos observar o segundo diagrama desenhado no passo 2 (direita). Vamos calcular o momento em relação ao ponto . Assumindo que o sentido positivo é o anti-horário, temos:
Como os ângulos e são muito pequenos, a seguinte aproximação se torna válida: . Assim, substituindo na expressão encontrada acima:
Resposta
Ei, a resposta está no passo a passo :)