Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 7.Problemas - Ex. 64
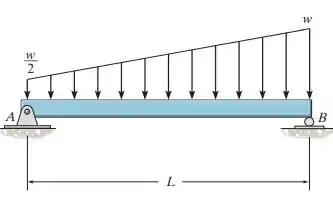
Determine os diagramas de força cortante e de momento fletor para a viga.
Passo 1
Fala, galera do RespondeAí. Tudo beleza? Bora para mais um exercício de Mecânica. Neste problema devemos determinar a os diagramas de momento fletor e esforço cortante para esta viga.
Primeiro, vamos esboçar o DCL:
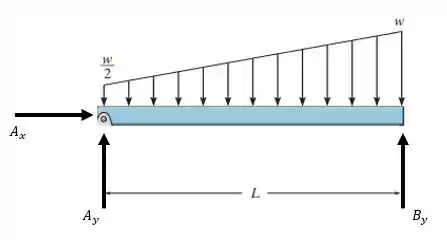
Podemos substituir esta carga distribuída por uma carga concentrada equivalente. Para isso, devemos dividir a carga na forma de trapézio em duas formas conhecidas. Fica assim:
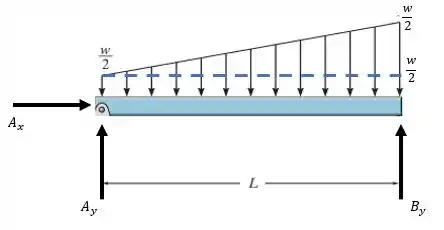
Ao traçarmos essa linha, vamos ficar com uma carga na forma retangular e outra na forma triangular. Primeiro, vamos substituir a carga retangular por uma carga na posição dada por:
E para a carga triangular, podemos substitui-la por uma carga concentrada em e ela pode ser encontrada assim:
Com isso, o nosso novo DCL vai ter a seguinte cara:
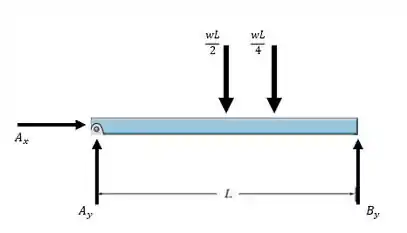
Passo 2
Em seguida, vamos utilizar a equação de momento no ponto para determinarmos a reação no apoio , temos:
Passo 3
Então, vamos calcular a força cortante e o momento fletor. Para isso, vamos analisar o que acontece quando fazemos um corte transversal na viga. Primeiro, para a porção da viga. Podemos esboçar esse DCL assim:
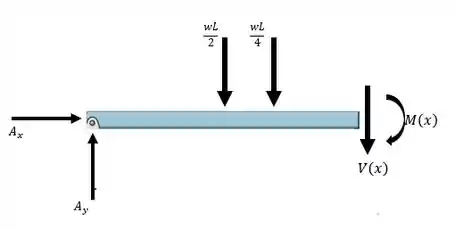
Com isso, vamos determinar o a força cortante e o momento fletor...
Pelo somatório das forças no eixo , temos:
E também, considerando o momento positivo girando no sentido anti-horário, vamos fazer o somatório dos momentos:
Passo 4
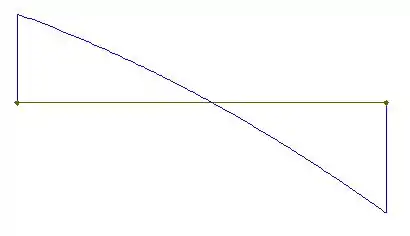
Assim, o diagrama de esforço cortante vai ser:
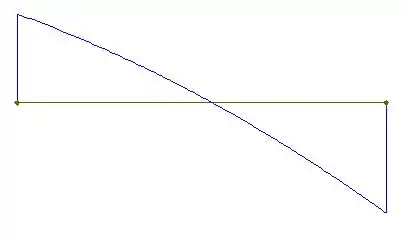
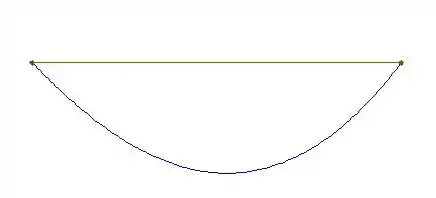
E o diagrama de momento fletor vai ter a seguinte cara:
Opa, é isso, galera. Bora praticar mais!!!
Resposta
