Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 7.Problemas - Ex. 86
Determine os diagramas de esforço cortante e de momento fletor para a viga composta.
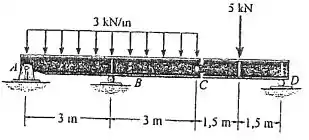
Passo 1
Para determinar os diagramas de esforço, em primeiro lugar as reações de apoio devem ser determinadas.
Em seguida, o eixo deve ser seccionado em posições a partir da extremidade esquerda que se estendem para partes entre forças, momentos ou carga distribuídas.
Para cada distância (espaço entre a extremidade esquerda e o ponto escolhido para seccionar), o diagrama de corpo livre deve ser feito indicando o esforço cortante e o momento fletor em suas convenções positivas, tal que é obtido através da soma das forças verticais e é obtido através da soma dos momentos em relação a extremidade esquerda.
Enfim, com os valores dessas duas variáveis determinadas é possível desenhar os diagramas de esforços.
Passo 2
Deve-se lembrar que a força resultante gerada por um carregamento retangular é dada por
E a posição do centroide é
Mas fazendo primeiro a análise da seção é possível obter o valor de uma das reações, tal que:
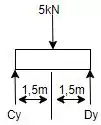
Então, considerando o sentido anti-horário como positivo e aplicando o princípio dos momentos em relação ao ponto :
Também, fazendo o somatório de forças para o eixo :
Agora, deve-se analisar o DCL de toda a viga para encontrar as outras reações de apoio. Logo, tem-se:
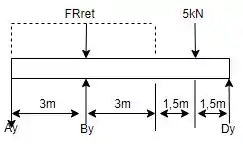
Com o princípio dos momentos em relação ao ponto e tendo o sentido anti-horário como positivo:
E com isso, fazendo o somatório de forças em :
Passo 3
Após determinar as reações, faz-se uma seção entre e e o DCL obtido será:
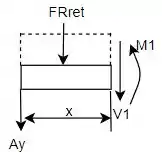
Tal intervalo analisado é .
Para determinar o esforço cortante aplica-se o somatório de forças no eixo vertical:
E para o momento fletor aplica-se o princípio dos momentos no ponto em que o eixo foi seccionado:
Para inserir estas informações nos diagramas de esforço, deve-se encontrar os valores nos extremos do intervalo. Logo:
Passo 4
Agora, pode-se fazer o mesmo processo para o intervalo seguinte dado por e que terá um DCL dado por:
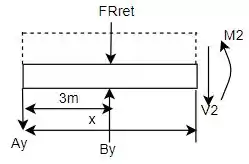
Para determinar o esforço cortante aplica-se o somatório de forças no eixo vertical:
E para o momento fletor aplica-se o princípio dos momentos no ponto em que o eixo foi seccionado:
Para inserir estas informações nos diagramas de esforço, deve-se encontrar os valores nos extremos do intervalo. Logo:
Passo 5
Novamente, pode-se fazer o mesmo processo para o intervalo seguinte dado por e que terá um DCL dado por:
Para determinar o esforço cortante aplica-se o somatório de forças no eixo vertical:
E para o momento fletor aplica-se o princípio dos momentos no ponto em que o eixo foi seccionado:
Para inserir estas informações nos diagramas de esforço, deve-se encontrar os valores nos extremos do intervalo. Logo:
Passo 6
Por fim é feito análise da última seção restante que se localiza entre a força de e o ponto para o intervalo seguinte dado por e que terá um DCL dado por:
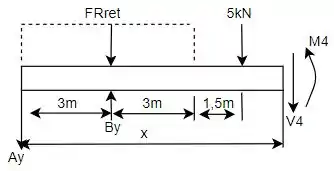
Para determinar o esforço cortante aplica-se o somatório de forças no eixo vertical:
E para o momento fletor aplica-se o princípio dos momentos no ponto em que o eixo foi seccionado:
Para inserir estas informações nos diagramas de esforço, deve-se encontrar os valores nos extremos do intervalo. Logo:
Passo 7
Portanto, inserindo os resultados do esforço cortante obtidos no diagrama tem-se:
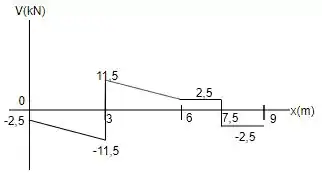
E para os resultados do momento fletor:
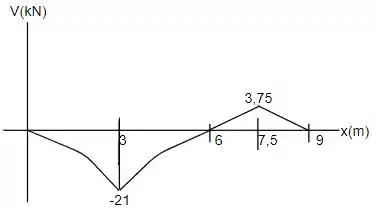
Resposta
