Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 5.Problemas - Ex. 45
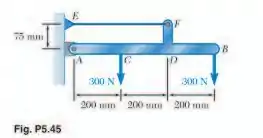
Trace os diagramas de força cortante e momento fletor para a viga e o carregamento mostrados na figura e determine o valor máximo absoluto (a) da força cortante e (b) do momento fletor.
Passo 1
Fala aí, galerinha. Tudo bem com vocês? Bora pra outra questão.
Esse braço na estrutura, equivale a força aplicada e um momento, que será a distância do braço multiplicada pela força. Esse momento será:
Logo, o momento será:
Portanto, o diagrama de corpo livre será:
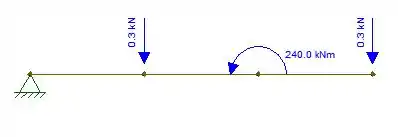
As reações de apoio serão determinadas pelas equações de equilíbrio. Logo:
Passo 2
Agora, basta traçar os diagramas. O diagrama de cortante será:
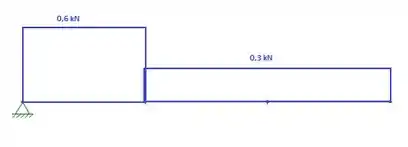
O de momento será:
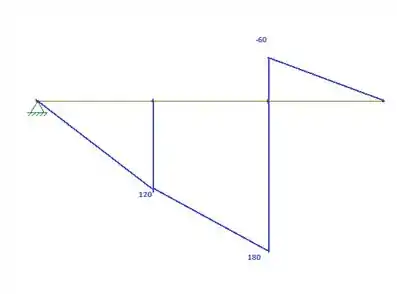
Logo:
Resposta
Exercícios de Livros Relacionados
Um tubo de aço com diâmetro de 101,6 mm deve suportar o carregamento mostrado na figura. Sabendo que o estoque de tubos disponíveis tem espessuras que variam de 6 mm e 24 mm em incrementos de 3 mm, e
Dois perfis U de aço laminado devem ser soldados entre si ao longo das extremidades das mesas para suportar o carregamento mostrado na figura. Sabendo que a tensão normal admissível para o aço utiliza
(a) utilizando funções de singularidade, encontre a intensidade e posição do máximo momento fletor a viga e carregamento mostrados, (b) determine a tensão normal máxima em razão da flexão.
A viga AB, consistindo em uma placa de alumínio de espessura uniforme b e comprimento L, suporta a carga mostrada. (a) sabendo que a viga tem resistência constante, expressa h em termos de x , Leh 0 n
Uma viga em balanço AB consistindo em uma placa de altura constante h e largura b variável suporta a carga concentrada P no ponto A. (a) sabendo que a viga é de resistência constante, expresse b em te