Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 5.Problemas - Ex. 114
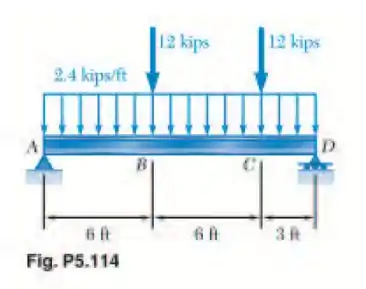
Uma viga está sendo projetada para ser vinculada e carregada conforme mostra a figura. (a) Usando funções de singularidade, encontre a intensidade e a localização do momento fletor máximo na viga. (b) Sabendo que a tensão normal admissível para o aço a ser utilizado é de 165 MPa, encontre o perfil de mesa larga mais econômico que pode ser utilizado.
Passo 1
Beleza! A primeira coisa que vamos fazer é desenhar o diagrama de corpo livre para a viga, dessa forma, o DCL será:
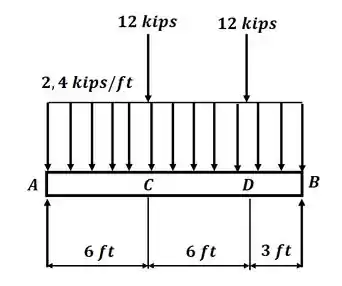
Com o DCL acima, podemos aplicar o somatório de momentos em relação ao ponto B e com isso encontrar a reação no ponto A. Então teremos:
Agora podemos escrever a equação para a força cortante, já que temos todas as forças aplicadas e os pontos onde são aplicadas, só lembrando que como temos carregamento distribuído, ele possui ordem 1 na equação de singularidade para a força cortante. Sendo assim, considerando a origem no ponto A, com , a equação para a força cortante será:
Passo 2
Agora, para encontrarmos a equação do momento fletor, como já temos a equação para a força cortante, basta lembrar que a derivada do momento equivale a força cortante, ou seja:
Isolando as variáveis dessa equação, temos:
Integrando essa expressão dos dois lados, teremos:
Agora, substituindo a expressão encontrada para no passo 1, a equação acima se torna:
Resolvendo a integral, teremos:
Em que é a constante de integração. Nesse caso, a constante de integração corresponde aos momentos localizados que são aplicados ao sistema, no nosso caso não temos nenhum momento localizado, então teremos:
Então a equação do momento será:
Passo 3
Agora para encontrar a tensão normal máxima, precisamos primeiro do momento máximo. Para isso, vamos igualar a derivada da função momento (que é a própria equação da força cortante) a zero, e encontrar a localização do momento máximo. Fazendo isso, teremos:
Nesse caso, como estamos trabalhando com a função de singularidade, precisamos dividir a função nos intervalos para calcular separadamente o valor de máximo para cada intervalo. Então, começando pelo primeiro intervalo, em teremos:
O valor de encontrado está fora do intervalo de análise, dessa forma não temos um ponto de máximo nesse intervalo. Vamos agora considerar o intervalo , onde teremos:
Opa! Achamos um valor dentro do intervalo de análise. Vamos ver agora se temos outro valor de máximo no último intervalo, em , então teremos:
Nããão! Esse valor também não está no intervalo de análise. Então o único valor possível será:
Essa é a localização do momento máximo. Agora para encontrar seu valor, basta substituir essa posição de na equação que encontramos para o momento lá no passo 2. Então, fazendo isso, teremos:
Passo 4
Beleza! Agora para a letra (b), nós sabemos que a tensão normal máxima provocada pelo momento fletor é dada por:
Como o enunciado nos pede o perfil de uma viga de mesa larga (viga W), podemos usar a propriedade módulo de resistência elástico do perfil, que é dado por:
Substituindo essa expressão na equação para a tensão, ela se torna:
Agora, vamos converter o valor de momento encontrado no passo 3 para unidades do sistema internacional, para que possamos comparar com os valores de W lá do apêndice C. Então, sabendo que:
Nosso momento será:
Então, agora vamos calcular o valor do módulo de resistência elástico que o perfil adequado deve ter, substituindo os valores conhecidos, chegamos em:
Como queremos o perfil mais econômico, devemos começar olhando os menores perfis, até chegar em um que possua no mínimo o módulo de resistência elástico encontrado. E, com esse valor de , lá do apêndice C, vemos que podemos utilizar o seguinte perfil:
Pois ele possui . Proonto! Conseguimos encontrar o perfil mais econômico para o nosso caso.