Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 6.Problemas - Ex. 13
Determine a força em cada elemento da treliça mostrada na figura.
Passo 1
Vamos começar o exercício analisando o nó A:
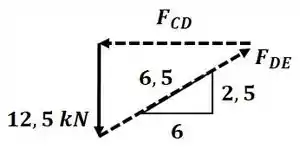
Aplicando semelhança de triângulos entre os triângulos de força e de comprimento, temos:
Pegando a primeira e terceira parcela, temos:
Pegando a segunda e terceira parcela, temos:
Agora vamos analisar o nó G:
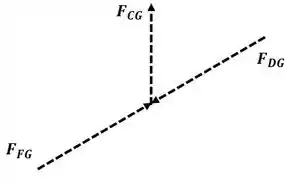
Agora aplicando o somatório de forças na direção :
E, aplicando agora o somatório de forças para a direção :
Passo 2
Agora vamos analisar o nó C:
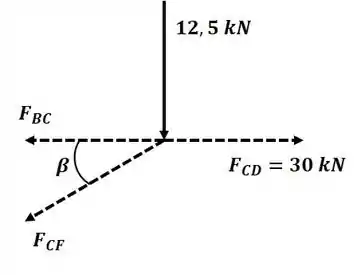
Para descobrir o valor de , precisamos encontrar o comprimento :
Agora, pode ser encontrado fazendo:
Aplicando o somatório de forças na direção :
Agora aplicando o somatório de forças na direção :
Agora vamos analisar o nó F:
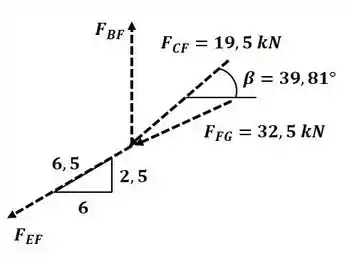
Agora aplicando o somatório de forças na direção :
Aplicando o somatório de forças na direção :
Passo 3
Agora vamos analisar o nó B:
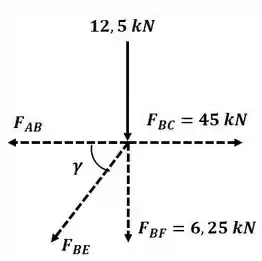
Precisamos encontrar o valor do ângulo , ele pode ser encontrado olhando para os comprimentos dos braços da treliça fazendo:
Aplicando o somatório de forças na direção :
Agora aplicando o somatório de forças na direção :
Agora, analisando o nó E:
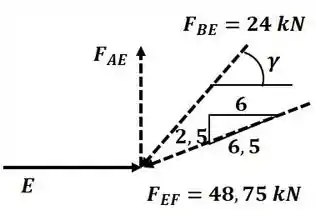
Aplicando o somatório de forças na direção :