Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 4.Problemas - Ex. 01
Determine a força em cada membro da treliça carregada.
Passo 1
Fala galera, tudo certo? Bora fazer mais um exercício? Prometo que vai ser bem rapidinho!
O enunciado nos pede para determinar a força que cada barra da treliça está submetida devido ao peso de adicionado no ponto . Antes de resolver, vamos fazer o diagrama de corpo da treliça para entender melhor o problema:
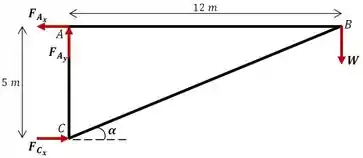
O primeiro passo é determinar as reações de apoio nos nós e que são como forças externas atuando na treliça. Em o apoio é do tipo pino, possui reação vertical e horizontal, e em é do tipo rolete, impede movimento apenas na horizontal. Uma vez que a treliça está em equilíbrio, podemos utilizar as equações de equilíbrio de forças e momento para determinar as reações de apoio. Começando pelo somatório de momentos em torno de , já que isso elimina duas das três incógnitas.
Para facilitar os cálculos, vamos também definir o ângulo de inclinação da barra em relação à horizontal.
Passo 2
Show, feito isso, podemos analisar separadamente os nós da treliça, que pela condição de equilíbrio devem ter os somatórios de forças e momentos nulos. Começando então pelo nó temos:
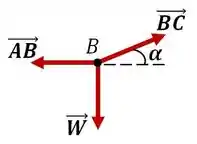
Onde significa que a barra está sendo tracionada, ou seja, tende a alongar e que a barra está sendo comprimida, tende a reduzir.
Passo 3
Sucesso até agora né?! Já temos as forças nas barras e , só precisamos descobrir então a força na barra que pode ser facilmente obtida pelo equilíbrio no nó .
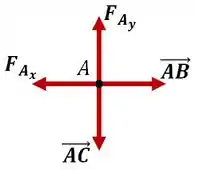
Ufa! Até que foi tranquilo né? Partiu pra próxima!
HYPERLINK "https://emojiterra.com/pt/rosto-piscando/" 