Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 6.Problemas - Ex. 54
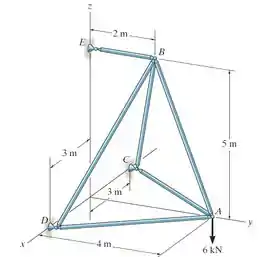
Determine a força em cada membro da treliça espacial e indique se os membros estão sob tração ou compressão. Dica: a reação de apoio em atua ao longo do membro . Por quê?
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!
Temos aqui o caso de uma treliça espacial. Aqui, nesta questão, precisamos determinar a força em cada barra e se os membros estão sob tração ou compressão.
A metodologia de análise é a mesma que no caso da treliça plana. Isto é, podemos utilizar o método dos nós ou das seções.
A grande diferença é que, por ter três dimensões para analisar as contas, elas acabam dando um pouco mais de trabalho, mas não é tanto assim.
Sendo assim, vamos as contas!
Passo 2
Vamos começar a questão determinando a direção de atuação das forças em cada barra.
Nosso objetivo final será escrever a força como um escalar multiplicado pelo versor de cada direção. Portanto, vamos começar escrevendo os versores de cada direção. Eles são:
Agora, que sabemos os versores de cada direção, podemos aplicar o método dos nós.
Passo 3
Vamos começar aplicando o método dos nós para o nó .
Como temos equilíbrio, pelo somatório de forças temos:
Resolvendo o sistema acima obtemos que e .
Como os versores foram definidos para ter extremidade final no ponto . Então, podemos dizer que as forças estão “apontando para o nó A”. Em outras palavras, as forças foram definidas como compressivas.
Sendo assim, se obtermos , temos forças compressivas. Caso contrário, forças trativas.
Portanto, as forças em cada membro serão:
Passo 4
Agora é só repetirmos o mesmo procedimento, só que para os outros nós! Vamos para o nó então!
Só devemos tomar um único cuidado! A força que obtivemos no Passo anterior deve mudar de sentido aqui, pois estamos analisando o outro extremo da barra.
Portanto, vamos escrever ao fazermos o nosso somatório.
Então, como temos equilíbrio, pelo somatório de forças temos:
Resolvendo o sistema acima obtemos que e .
Relembrando, se obtermos , temos forças compressivas. Caso contrário, forças trativas.
Portanto, as forças em cada membro serão:
E assim finalizamos a questão!