Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 6.Problemas fundamentais - Ex. 1
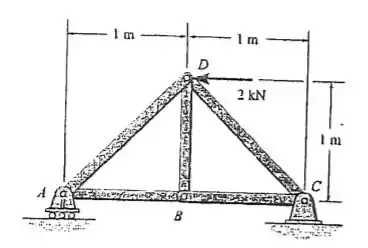
Determine a força em cada membro da treliça. Indique se os membros estão sob tração ou compressão.
Passo 1
E aí galerinha, como vocês estão?
Vamos lá, nesse problema nós desejamos encontrar as forças em cada membro da treliça e, para isso, vamos primeiramente fazer um diagrama de corpo livre decompondo todas as forças presentes nessa nossa estrutura, ficamos, assim, com
Tendo o diagrama acima em mãos, vamos calcular as nossas reações de apoio usando o fato de que nossa treliça está em equilíbrio, ou seja, o somatório das forças que atuam na mesma deve dar zero. Dessa forma, teremos
Adotando o sentido anti-horário como positivo vamos ter
Então, da equação podemos concluir que . Lembrando que o sinal de negativo está nos indicando que a força está na direção contrária da que adotamos inicialmente.
Passo 2
Agora a gente pode analisar os nós, começando pelo nó A.
Note que todos os ângulos da treliça são 45 graus, devido ás dimensões.
Analisando, na sequência, as forças que atuam no eixo vamos encontrar
Dessa forma vamos ter
Tá ficando interessante o negócio por aqui, né? Dá até um orgulho quando vai tudo batendo certinho.
Já que tá dando certo vamos continuar fazendo essa mesma análise, só que agora para o nó de tal forma que vamos encontrar
Fazendo o somatório das forças agora em fica mamão com açúcar olha só
Passo 3
Pronto, dá uma respirada aí que agora é o gran finale, pra gente fechar com chave de ouro essa questão. Vamos repetir a mesma forma de análise, mas agora para o nó de tal forma que encontramos