Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 4.Problemas Fundamentais - Ex. 38
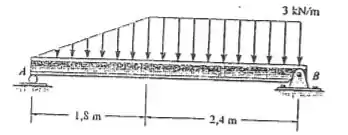
Determine a força resultante e especifique onde ela atua na viga, medindo a partir do ponto .
Passo 1
Fala, querido! Queremos a posição da força resultante desse carregamento distribuído em relação a .
A ideia aqui é que a gente pode substituir os carregamentos distribuídos por cargas concentradas. E essas cargas concentradas ficam na linha que passa pelo centroide da figura que representa o carregamento.
Por exemplo, nosso carregamento tem cara de triângulo até e depois tem cara de retângulo. Algo assim:
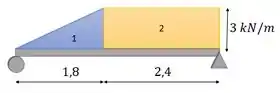
Para a achar a força equivalente a cada um desses carregamentos distribuídos, a gente vai achar a área dessas figuras, com base nos dados dessa figura. Aí a área vai ser igual a força resultante causada pelo carregamento.
A força equivalente ao carregamento retangular vai ser
E a força resultante do carregamento triangular vai ser
Passo 2
Agora vamos achar a posição de cada uma dessas forças. Como vimos, elas vão estar na coordenada horizontal do centroide das figuras que representam os carregamentos.
Para o retângulo, o centroide é no centro dele. Então a coordenada horizontal do centroide dele é na metade do seu comprimento. Em relação a , a posição seria:
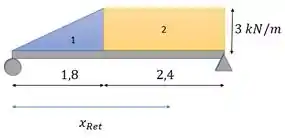
Já para o triângulo, a coordenada horizontal do centroide é a 1/3 da base do triângulo, ou a 2/3 da ponta do triângulo. Geometricamente, esses valores nos dão o mesmo ponto. Mas é mais fácil para a gente achar o centroide a partir da ponta do triângulo né? Já que ela é o ponto .
Então, achamos:
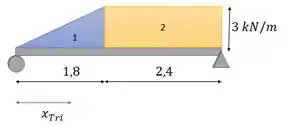
Posicionando nossas forcinhas na viga:
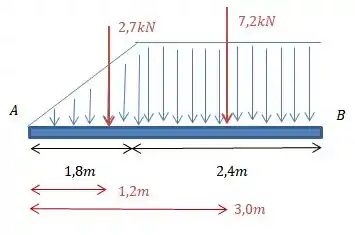
Em azul, é o nosso primeiro momento, é a carga distribuída. E em vermelho, é o nosso segundo momento, depois que a gente tirou as cargas distribuídas e deixou só as cargas concentradas resultantes.
Passo 3
Só que queremos reduzir essas duas forças a uma força resultante só. Então precisamos fazer mais umas coisinhas.
Vamos calcular a nossa força resultante geral somando as duas que a gente achou:
O sinal negativo indica que a força está apontando para baixo.
E a posição dela a gente vai achar o usando o princípio dos momentos. As forças no nosso sistema atual, as concentradas, precisam gerar o mesmo momento em que a força resultante geral sozinha na posição dela, também em relação a .
Onde esse somatório é o somatório de momentos causados pelas forças concentradas em relação a . E é o momento causado por , estando distante de .
E adotando o sentido anti-horário como positivo:
Substituindo os dados
Encontrando o nosso ...
Sendo assim, a nossa resultante dada por esse carregamento, é aplicada a do ponto .