Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.4 - Ex. 53
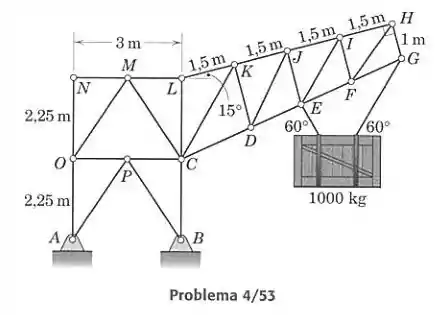
Determine a força no elemento da treliça carregada.
Passo 1
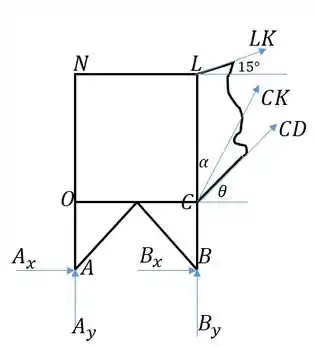
Vamos resolver esse problema pelo método das seções, fazendo um corte na treliça e pegando uma parte dela para considerar como um corpo rígido. Como estamos interessados no elemento , vamos fazer um corte passando por ele, e pegar o lado esquerdo da treliça. Nosso corte passará por , e :
Passo 2
Primeiramente vamos aplicar equações de equilíbrio para a treliça como um todo, para encontrar as reações em e . Como os dois fios que seguram a carga de 1000 kg fazem 60° com a horizontal, temos:
Pela soma das forças horizontais:
Agora as veticais:
Para encontrar , precisamos calcular o momento em torno de da treliça inteira. Mas pra isso precisamos das distâncias dos pontos e onde estão aplicadas as trações para o ponto , então vamos calcular as coordenadas dos pontos.
Passo 3
Vamos então considerar que e tem coordenadas (0, 0) e (0, 2.25 m) e calcular as coordenadas de e .
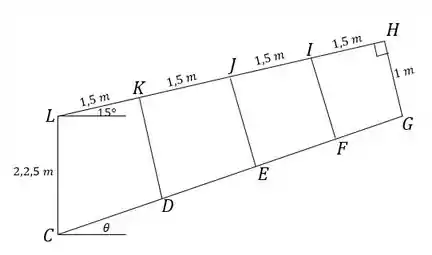
Primeiro vamos descobrir quanto é o ângulo . A tangente é a distância vertical sobre a distância horizontal entre e :
A inclinação da linha de baixo em relação à de cima é . Então o tamanho de , e é igual a:
Então conseguimos achar as coordenadas de através das coordenadas de . Sabemos que as de são:
Então achamos as de :
Passo 4
Agora que temos todas as distâncias horizontais e verticais dos pontos , e até o ponto e o valor das trações , conseguimos achar através do momento em relação a .
Substituindo os valores:
O valor negativo indica que é para baixo a força vertical em . Então, voltando à equação que encontramos no passo 2:
Passo 5
Pronto, agora que já fizemos isso tudo para achar as forças e , podemos voltar pra nossa seção da treliça e calcular :
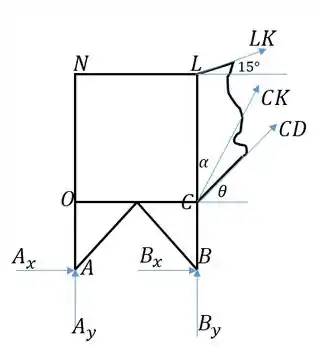
O ângulo é calculado também através de sua tangente, que é a distância horizontal sobre a distância vertical entre e . As coordenadas de são:
Então achamos :
Como temos duas forças desconhecidas passando em , primeiro vamos fazer o momento em relação a esse ponto:
Agora achamos fazendo as somas das forças horizontais e verticais:
Como :
Isolamos para substituir na próxima equação:
Substituímos agora o valor de encontrado na equação anterior:
O valor negativo indica que a força é de compressão do elemento e não de tração como foi desenhado.