Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.10 - Ex. 216d

Esboce os diagramas de cortante e de momento para cada uma das quatro vigas carregadas e apoiadas como mostrado.

Passo 1

  1. A terceira viga pode ser dividida em 3 regiões de comprimento l / 3 : antes do primeiro apoio, entre os dois apoios e depois do segundo. Primeiro vamos calcular as forças externas nos apoios 1 e 2. Pelo equilíbrio vertical, as forças tem o mesmo módulo P e sentidos contrários. Pelo tipo de apoio, podemos ver que o da esquerda só pode fazer força para cima, então o da direita faz força para baixo. Fazendo o momento em torno da extremidade esquerda:

∑ M = 0 ⇒ M + P l 3 - P 2 l 3 = 0 ⇒ M - P l 3 = 0 ⇒ M = P l 3 ⇒ P = 3 M l

Passo 2

Agora vamos analisar as três regiões. Fazemos um corte a uma distância x da extremidade esquerda. E analisamos o trecho a esquerda do corte:

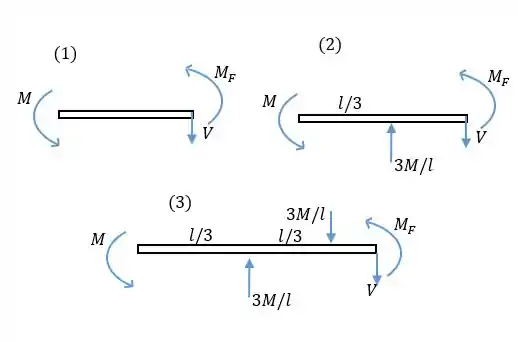
Aplicando o somatório das forças verticais e o momento no ponto de coordenada x , achamos V e M . Na primeira região. Temos:

∑ F y = 0 ⇒ V x = 0

∑ M = 0 ⇒ M F ( x ) = 0

Na segunda:

∑ F y = 0 ⇒ V x = 3 M l

∑ M = 0 ⇒ M F x = 3 M l x - l 3 = 3 M l x - M

Na terceira:

∑ F y = 0 ⇒ 3 M l - 3 M l - V = 0 ⇒ V x = 0

∑ M = 0 ⇒ - 3 M l x - l 3 + 3 M l x - 2 l 3 + M F = 0  

⇒ - 3 M l x + M + 3 M l x - 2 M + M F = 0 ⇒ M F x = M

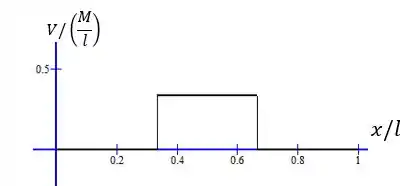
Com isso, esboçamos os diagramas de V e M F . V é constante e igual a 0 , depois constante igual a M l 3 e depois volta a ser zero. Representamos o gráfico de V / M l   por x / l :

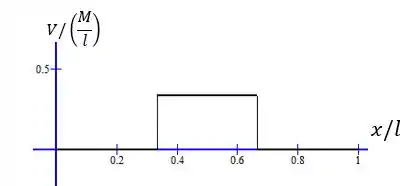
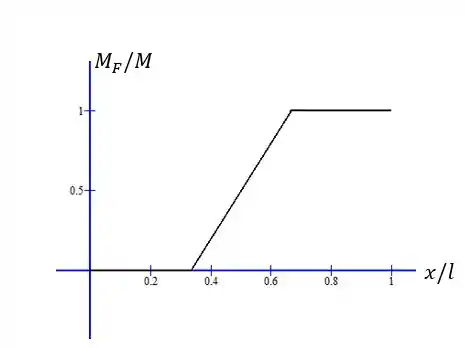
M F é zero, depois cresce linearmente a uma taxa 3 M L e depois fica constante e igual a M . Representamos o gráfico de M F / M por x / l :

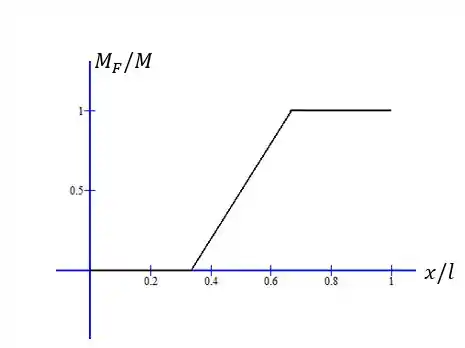
Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

118- Determine o cortante V na seção B, localizada entre A e c, e o momento M no apoio A.
117- Determine as distribuições da força constante e do momento fletor produzidos na viga pela carga concentrada. Quais são os valores do cortante e do momento em x = l / 2 ?
119- Desenhe os diagramas de cortante e de momento do trampolim, que sustenta o homem pesando 80 kg, preparado para mergulhar. Especifique o momento fletor de máximo módulo.
120- Desenhe os diagramas de cortante e de momento para a viga carregada em seu ponto médio pelo momento C
121- Desenhe os diagramas de cortante e de momento para a viga submetida a um momento em sua extremidade. Qual é o valor do momento em uma secão 0.5m a direita de B?