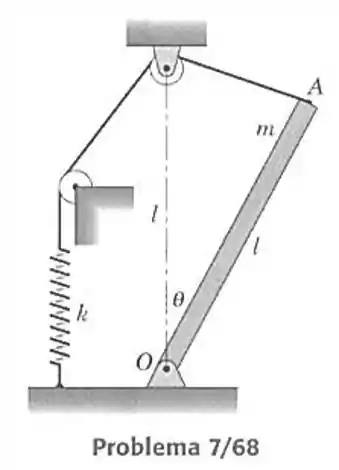
68- A figura mostra a vista lateral de uma claraboia uniforme de massa e com centro de massa na metade da distância entre e . A clarabóia é contrabalançada pela ação da mola, que tem uma rigidez e que não está alongada quando elas está no plano vertical, em . Determine a rigidez necessária para equilibrar a clarabóia em uma posição de equilíbrio para .

Vamos desenhar o sistema de modo que sejamos capazes de ver a variação da energia elástica e da potencial gravitacional.

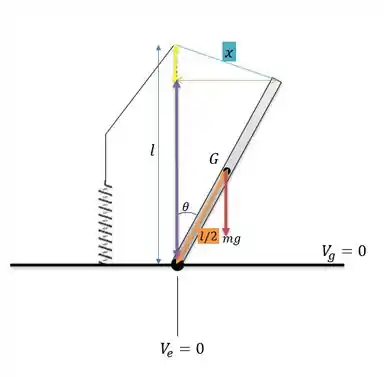
De modo que traçamos as retas que nos dão as posições onde o sistema de energia potencial gravitacional e energia potencial elástica nula.

Se espelharmos a reta laranja na vertical ,que nos diz a distância da altura do centro gravitacional barra, nós teremos a energia potencial gravitacional do sistema que será igual a:

Agora para a energia potencial gravitacional, nós temos que quando a mola não se estica, o que nos diz que a distância da figura é igual a zero, logo é a deformação da mola.

Porém como calcular o valor de , bem... é a hipotenusa do triângulo retângulo formado pelo cateto verde e pelo cateto amarelo.

Espelhando a barra toda na vertical e na horizontal temos que a reta roxa vale , assim como feito para a energia potencial. E a reta verde vale . Logo a reta amarela vale a diferença:

Fazendo Pitágoras nesses dois catetos temos:

Explicitando :

Abrindo a parcela

Como a energia potencial elástica do sistema é dada pela fórmula:

Logo:

Então a energia total do sistema será: