Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 8.Problemas fundamentais - Ex. 3
Determine a força máxima que pode ser aplicada sem fazer com que as duas caixas de se movam. O coeficiente de atrito estático entre cada caixa e o piso
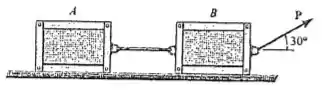
Passo 1
Desejamos encontrar o valor máximo de de tal forma que as caixas não e movam. Para isso vamos tomar as duas caixas como um sistema único e assim, podemos traças o seguinte diagrama de corpo livre
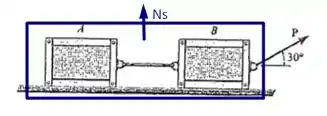
Onde nossa força de atrito vai estar contra o sentido do movimento, ou seja, vai estar para a esquerda. Além disso, ela é dada por
Passo 2
Na iminência da movimentação das caixas nós teremos
Resposta
Exercícios de Livros Relacionados
A bobina com massa de 150k g se apoia sobre o piso em A e contra a parede em B. Determine a força P necessária para iniciar o desenrolar do fio horizontal para fora da bobina. O coeficiente de atrito
O disco de 45k g se apoia sobre a superfície para a qual o coeficiente de atrito estático é u=0,2 . Determine o maior momento de binário M que pode ser aplicado à haste sem causar movimento.
O dispositivo de travamento por atrito é fixado por um pino em A e se apoia contra a roda em B. Ele permite a liberdade de movimento quando a roda está girando em sentido anti-horário em relação a C.
O disco de 45k g se apoia sobre a superfície para a qual o coeficiente de atrito estático é u=0,15 . Se M=50N m , determine a força de atrito em A .
Resolva o Problema 8.22 se o momento de binário M 0 for aplicado em sentido anti-horário.