Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 11.Problemas - Ex. 55

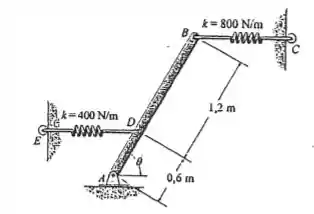
A barra uniforme A B pesa 500 N . Se as duas molas D E   e   B C estão livres quando θ = 90 ° , determine o ângulo θ para equilíbrio usando o princípio da energia potencial. Investigue a estabilidade na posição de equilíbrio. As duas molas sempre permanecem na posição horizontal, devido as guias de rolete em C   e   E .

Passo 1

Desejamos encontrar o valor de θ para encontrarmos o equilíbrio utilizando o princípio da energia potencial. Primeiramente, vamos fazer a conversão de algumas unidades de tal forma que fique mais simples nossa análise e como estamos trabalhando com os ângulos em graus, no fim das contas não fará diferença essa troca pois devemos chegar no mesmo resultado. Assim

k = 400 N m = 2 l b i n ,   k = 800 N m = 4 l b i n

1,2 m = 4 f t   ,   0,6 m = 2 f t

Dessa forma, utilizando o princípio da energia potencial vamos ter

U = U E + U G

U = ∑ k x 2 2 + W ⋅ y

= 1 2 ⋅ 24 ⋅ 2 ⋅ cos ⁡ θ 2 + 1 2 ⋅ 48 ⋅ 6 ⋅ cos ⁡ θ 2 + 100 ⋅ ( 3 ⋅ sin ⁡ ( θ ) )

= 912 ⋅ cos 2 ⁡ θ + 300 ⋅ s i n ⁡ ( θ )

Passo 2

Para o equilíbrio devemos ter d V d θ = 0 . Assim teremos

0 = - 1824 ⋅ s i n θ ⋅ cos ⁡ θ + 300 ⋅ c o s θ = 0 → θ = 90 °   o u   θ ≈ 9,47 ° .

Testando a segunda derivada para cada um desses pontos encontrarmos que para o primeiro ponto temos um valor maior do que 0 e, portanto, é um ponto de equilíbrio estável. Enquanto que para o segundo ponto temos um valor menor do que 0 como resultando e, assim, esse ponto é de equilíbrio instável.

Resposta

θ = 90 °   o u   θ = 9,47 ° .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma ligação uniforme AB tem massa de 3 kg e está conectada nas duas extremidades por meio de pinos. A barra BD, com peso desprezível, passa por um bloco giratório em C. Se a mola tem uma rigidez k = 1
Determine os ângulos θ para haver equilíbrio do cilindro de 100 kg e investigue a estabilidade em cada posição. A mola tem uma rigidez de k = 6 k N m e um comprimento livre de 225 mm
Se uma carga l de 10 kg é colocada na panela, determine a posição x do bloco H de 0,75 kg para haver equilíbrio. A balança está em equilíbrio quando não há peso nem carga na balança.
Se o mecanismo está em equilíbrio quando θ = 30 º º, determine a massa da barra BBC. A mola tem uma rigidez k = 2 kN/m e está livre quando θ = 0 º º. Despreze a massa das ligações
O cilindro é feito de dois materiais de modo que tem uma massa m e um centro de gravidade no ponto G. Mostrre que, quando G se encontra acima do centroide C do cilindro, o equilíbrio é instável.