Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 8.Problemas - Ex. 101
Se a tração na mola é , determine o maior momento de binário que pode ser aplicado à roda sem fazer com que ela gire. O coeficiente de atrito estático entre a correia e a roda é e entre a correia e o gancho . A polia está livre para girar.
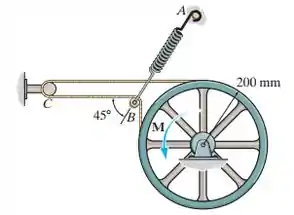
Passo 1
Analisando a roda, temos:
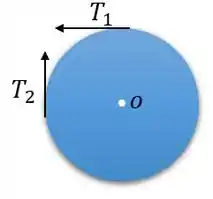
Considere que nosso momento máximo será :
Logo,
Passo 2
Agora vamos analisar o atrito entre a roda e a correia. Para isso vamos usar a seguinte relação:
Nosso é , pois medimos no sentido anti-horario. Logo,
Fazendo as conta:
Analisando o ponto . No eixo horizontal, temos:
Logo,
Passo 3
Agora vamos usar a equação .
Assim,
Voltando em :
Resposta
Exercícios de Livros Relacionados
112. Um freio de cinta é utilizado para controlar a velocidade de um volante, conforme mostra a figura. Os coeficientes de atrito são μ s = 0,30 e μ k = 0,25 . Determine a intensidade do torque que de
Se θ = 30 ° , determine o menor coeficiente de atrito estático em A e B de modo que o equilíbrio da estrutura de suporte seja mantido, independentemente da massa do cilindro. Desconsidere a massa das
Determine a força horizontal P máxima que pode ser aplicada à argola de 12k g sem fazer com que ela gire. O coeficiente de atrito estático entre a argola e as superfícies em A e B é μ s = 0,2 . Consid
Se o coeficiente de atrito estático em A e B é μ s = 0,6 , determine o ângulo máximo θ para o sistema permanecer em equilíbrio, independentemente da massa do cilindro. Desconsidere a massa das hastes.
O disco de 100k g se apoia em uma superfície para a qual μ B = 0,2 . Determine a menor força vertical P que pode ser aplicada tangencialmente ao disco que causará o movimento iminente.