Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 8.Problemas - Ex. 68
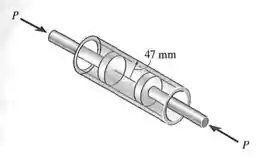
Determine a força máxima P que pode ser exercida em cada um dos dois pistões de modo que a componente da tensão circunferencial no cilindro não ultrapasse 3 MPa. Cada pistão tem raio de 45 mm e a espessura da parede do cilindro é 2 mm.
Passo 1
Essa questão é basicamente o inverso da anterior
Primeiro calculamos a pressão gerada pelas forças, usando a relação com a tensão circunferencial no cilindro abaixo.
Passo 2
Assim descobrimos P multiplicando pela área do pistão
Resposta
Exercícios de Livros Relacionados
O painel de sinalização uniforme pesa 7,5 kN e é suportado pelo tubo AB que tem raio interno de 68 mm e raio externo de 75 mm. Se a parte frontal do painel estiver sujeita a uma pressão uniforme do ve
O eixo de 18 mm de diâmetro é submetido à carga mostrada na figura. Determine as componentes da tensão no ponto A. Trace um rascunho dos resultados em um elemento de volume localizado nesse ponto. O m
O guindaste AB consiste em tubo que é usado para levantar o feixe de hastes que tem massa total de 3 Mg e centro de massa em G. Se o tubo tiver diâmetro externo de 70 mm e 10 mm de espessura de parede
A barra tem diâmetro de 40 mm. Se sua extremidade for submetida às duas componentes de força mostradas na figura, determine o estado de tensão no ponto A e mostre os resultados em um elemento de volum
A haste maciça está sujeita à carga mostrada na figura. Determine o estado de tensão desenvolvido no material no ponto A e mostre os resultados em um elemento de volume diferencial nesse ponto.