Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 8.Problemas - Ex. 43
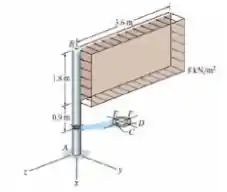
O painel de sinalização uniforme pesa 7,5 kN e é suportado pelo tubo AB que tem raio interno de 68 mm e raio externo de 75 mm. Se a parte frontal do painel estiver sujeita a uma pressão uniforme do vento p = 8 kN/m², determine o estado de tensão nos pontos C e D. Mostre os resultados em um elemento de volume diferencial localizado em cada em desses pontos. Despreze a espessura do painel de sinalização e considere que ele está apoiado ao longo da borda do tubo.
Passo 1
Oi oi, meu xuxuzinho!! Tudo bem com você?
Saca só, nosso enunciado nos diz que essa placa pesa e recebe um vento de frente com carga igual a , e nos pede o estado de tensão nos pontos C e D da seção transversal. Nem parece tão difícil, é só a gente olhar para aquele ponto lá de cima e fazer. Partiu!
Passo 2
Nosso primeiro passo será analisar essa carga distribuída pelo vento e transformá-la numa carga aplicada no centro da placa.
Como sabemos a força externa dela é igual a , vamos calcular nossas forças internas, ou seja, a normal, os momentos (afinal, temos nos 3 eixos) e o cortante, então para a soma das forças em :
Obtemos que:
E para o eixo :
Maravilha, agora podemos repetir o procedimento para os momentos, no caso para o eixo , obtemos que:
E para o eixo :
E por ultimos, para o momento no eixo , vamos descobrir que:
Com TODAS as forças calculadas, agora vamos partir pra cima do nosso .
E por outro lado, teremos:
Passo 3
Agora que já temos todo o necessário para calcular nossas tensões, por que vamos esperar?? Só bora comigo. Para , vamos ter que:
Da mesma maneira, para :
Sendo assim, será dado como:
Enquanto será:
