Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 8.Problemas - Ex. 66
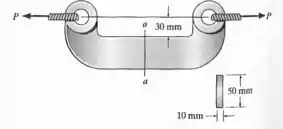
Determine o valor da carga P que provocará a tensão
normal máxima = 200 MPa na seção a-a do elo.
Passo 1
Somatório de força e momento na seção a-a
Assim o diagrama de corpo livre fica:
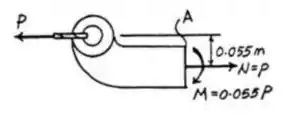
Passo 2
Obter em função de P:
Onde C é igual a distância da extremidade até o centroide da seção transversal e “I” o momento de inércia.
Resposta
Exercícios de Livros Relacionados
A barra tem diâmetro de 40 mm. Se sua extremidade for submetida às duas componentes de força mostradas na figura, determine o estado de tensão no ponto B e mostre os resultados em um elemento de volum
A haste maciça está sujeita à carga mostrada na figura. Determine o estado de tensão desenvolvido no material no ponto B e mostre os resultados em um elemento de volume diferencial nesse ponto.
O guindaste AB consiste em tubo que é usado para levantar o feixe de hastes que tem massa total de 3 Mg e centro de massa em G. Se o tubo tiver diâmetro externo de 70 mm e 10 mm de espessura de parede
O eixo de 18 mm de diâmetro é submetido à carga mostrada na figura. Determine as componentes da tensão no ponto B. Trace um rascunho dos resultados em um elemento de volume localizado nesse ponto. O m
O painel de sinalização está sujeito à carga uniforme do vento. Determine as componentes da tensão nos pontos C e D no poste de sustentação de 100 mm de diâmetro. Mostre os resultados em um elemento d