Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 6.Problemas - Ex. 34
Determine a força nos membros e da treliça de ponte Baltimore e indique se os membros estão sob tração ou compressão. Além disso, indique todos os membros de força zero.
Passo 1
Falaaaaaa pessoal, show de bola??
Bora resolver esse exercício na maciotaaaaa, então siimboraa!!
Vamos começar analisando o diagrama de corpo livre da treliça.
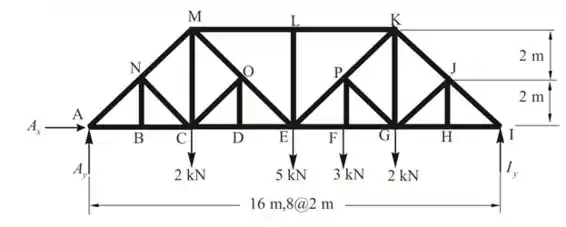
Passo 2
Por equilíbrio
Tomemos o momento sobre I
Passo 3
Na junta B
Passo 4
Da equação de equilíbrio
Portanto, a força no membro BN é zero
Passo 5
Na junta N
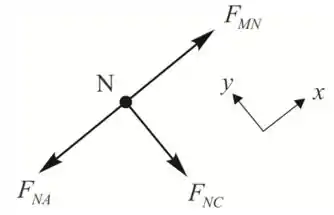
Passo 6
Da equação de equilíbrio
Portanto, a força no membro NC é zero
Passo 7
Na junta D
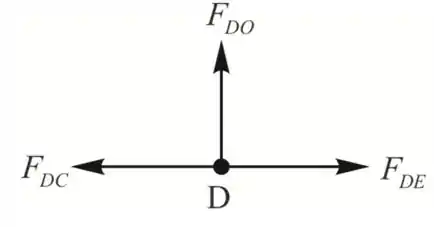
Passo 8
Da equação de equilíbrio
Portanto, a força no membro OD é zero
Passo 9
Na junta O
Da equação de equilíbrio
Portanto, a força no membro CO é zero
Passo 10
Na junta L
Passo 11
Da equação de equilíbrio
Portanto, a força no membro LE é zero
Passo 12
Na junta H
Passo 13
Da equação de equilíbrio
Portanto, a força no membro JH é zero
Passo 14
Na junta J
Passo 15
Da equação de equilíbrio
Portanto, a força no membro JG é zero
Passo 16
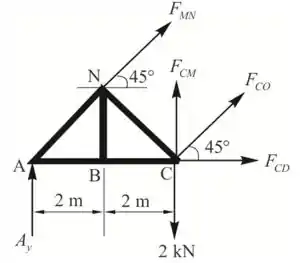
Passo 17
Vamos tomar alguns momentos sobre C
Passo 18
Vamos aplicar a equação de equilíbrio na direção
Portanto, a força no membro CD é de .
Passo 19
Vamos aplicar a equação de equilíbrio na direção
Portanto, a força no membro CM é
Resposta
Portanto, a força no membro LE é zero.
Portanto, a força no membro JH é zero.
Portanto, a força no membro JG é zero.
Portanto, a força no membro CD é de .
Portanto, a força no membro CM é