Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 5.Problemas - Ex. 77
O membro é sustentado por um pino em e um cabo . Se o cilindro tem massa de , determine as componentes das reações nesses pontos de apoio.
Passo 1
Falaaa... belezinha??
Nessa questão vamos ter que determinar as componentes das reações nos pontos de apoio da figura:
Coisa a beça, né??
E vamos achar isso tudo só com o somatório das forças em cada direção igual a zero:
E dos momentos também:
Passo 2
Vamos começar montando um diagrama de corpo livre maroto pra organizar tudo:
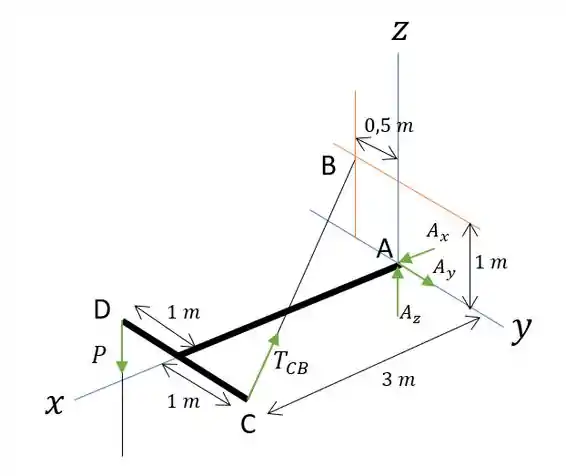
Já de cara a gente achar essa corda CB atravessadona e que pode dar um certo trabalho pra decompor essa força de tração. Maaass vamos representar na forma de vetor mesmo que fica arrumadinho e a gente não erra bobeirinha:
O vetor a gente acha fazendo:
E o módulo:
O vetor da tração fica:
Aproveitando pra calcular e colocando em vetor:
Passo 3
Agora vamos montar os somatórios de força em cada direção:
E para os momentos:
Detalheee aqui que não tem porque as forças são iguais (só ver o somatório de forças em ) e as distâncias também são iguais. Daí esse .
Passo 4
Pois muito que bem... Agora é só lutar pra resolver esse monte de equação.
Como não somos bobos nem nada... Vamos pegar o momento em(porque só tem uma incógnita):
Esse aparece em todas as equações, né??
Então agora é só felicidade achando as outras incógnitas.
Forças em :
Forças em :
Forças em :
Momento em :
Momento em :
Ufaaaa... conseguimos achar tudo.
Bora pra próxima questão?